基于MATLAB的随机信号及其参数建模分析.pdf

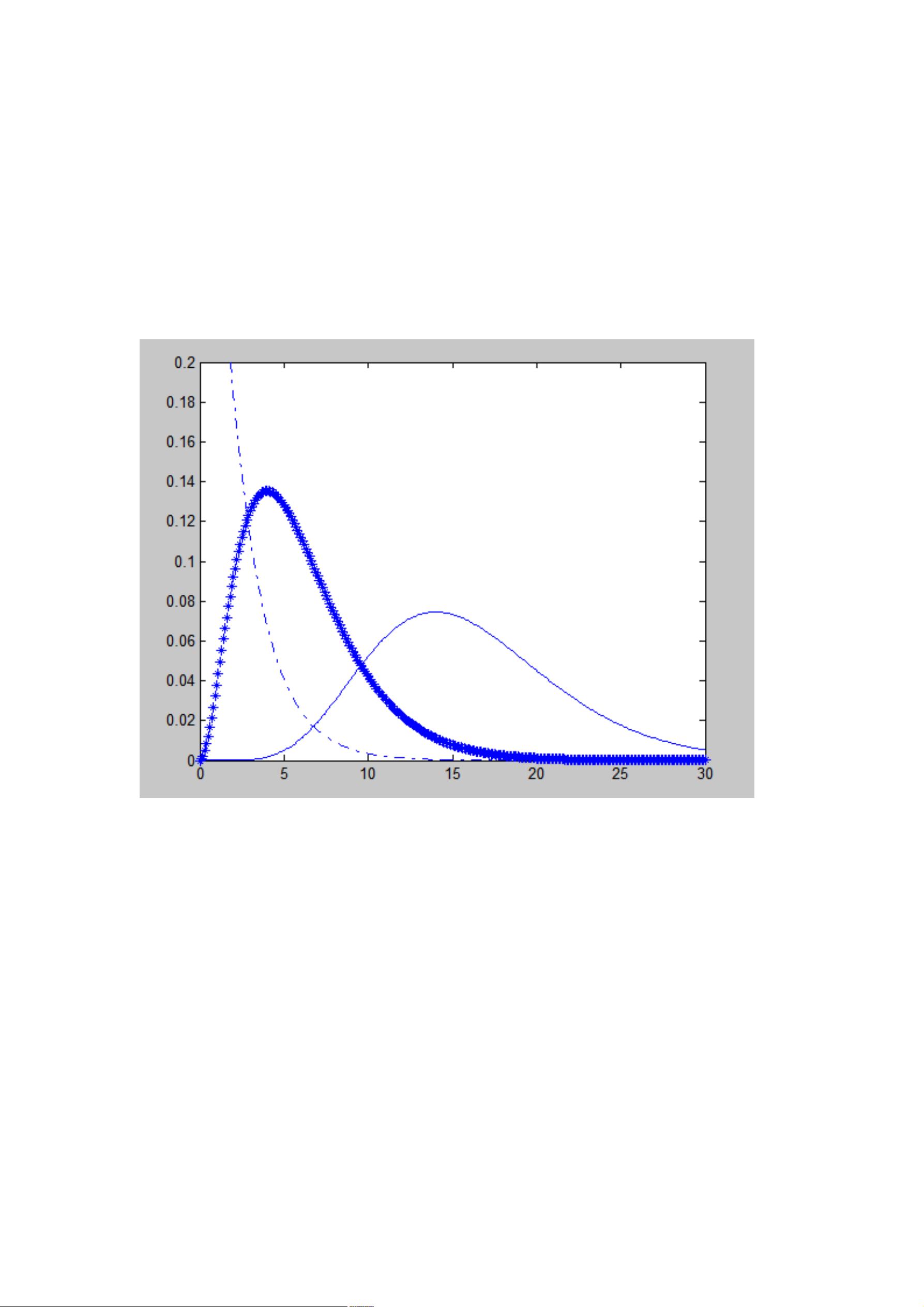
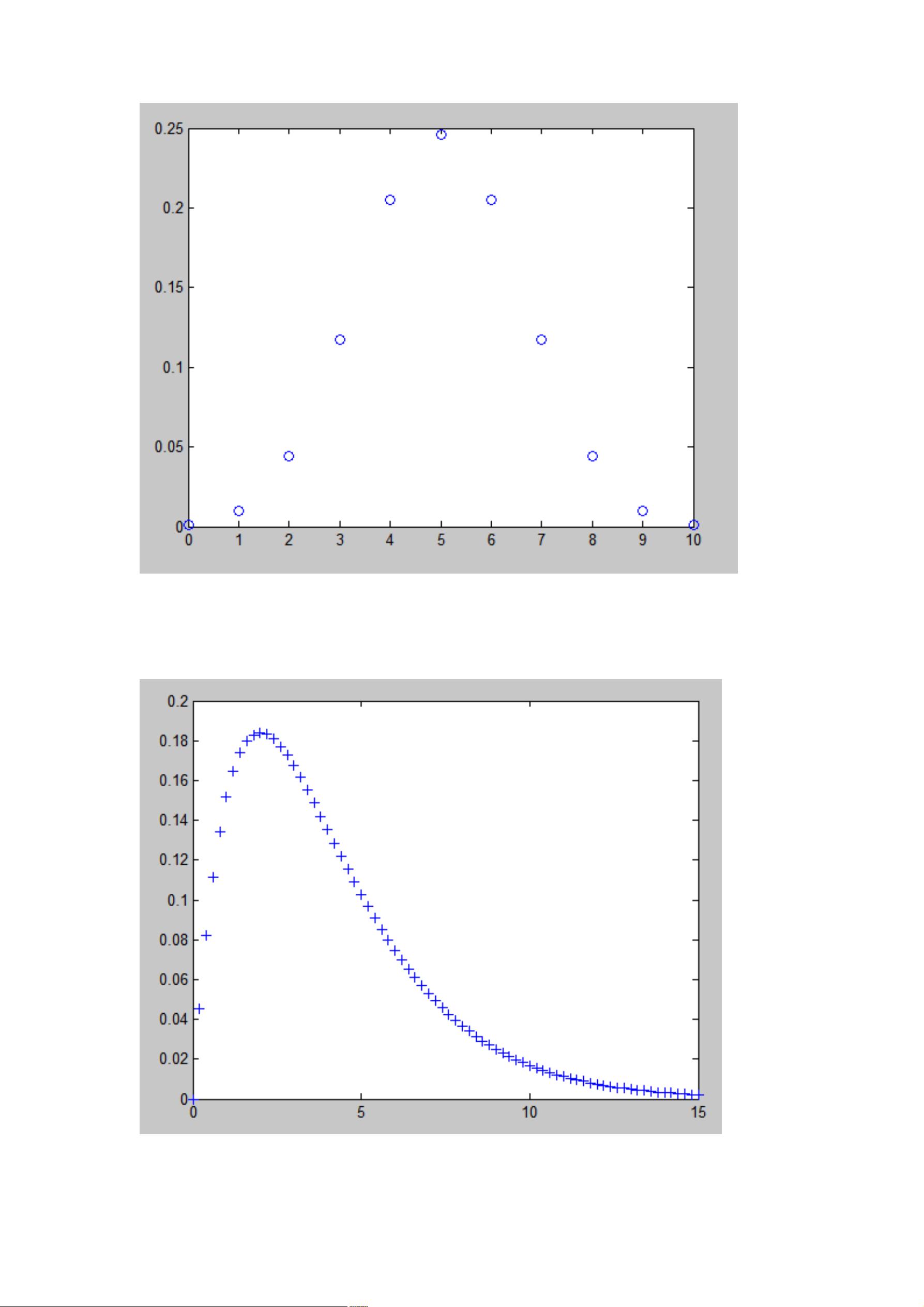
在MATLAB中，随机信号的建模和分析是信号处理和统计建模的重要部分，尤其在通信、控制、图像处理等领域广泛应用。以下是一些基于MATLAB进行随机信号及其参数建模的关键知识点： 1. **随机变量生成**： - `binornd` 函数用于生成二项分布的随机数。例如，`binornd(n,p)` 会产生 `n` 次独立的伯努利试验，每次试验成功的概率为 `p`。在示例中，我们看到不同维度和大小的参数设置。 - `normrnd` 函数则用于生成正态分布的随机数。`normrnd(mu,sigma)` 会生成平均值 `mu` 和标准差 `sigma` 的正态分布随机数。 2. **正态分布操作**： - `pdf('norm',x,mu,sigma)` 计算正态分布的密度函数值，其中 `x` 是点的位置，`mu` 是均值，`sigma` 是标准差。 - `random('norm',mu,sigma,n,m)` 生成一个 `n` 行 `m` 列的矩阵，每个元素都是均值为 `mu`、标准差为 `sigma` 的正态分布随机数。 3. **其他分布的生成与计算**： - `chi2pdf(x,df)` 计算卡方分布的密度函数，`x` 为点的值，`df` 为自由度。 - `ncx2pdf(x,df1,df2)` 用于生成非中心卡方分布的随机数。 - `exppdf(x,lam)` 计算指数分布的密度函数，`lam` 是率参数。 - `fpdf(x,df1,df2)` 计算F分布的密度函数，`df1` 和 `df2` 分别是第一和第二自由度。 - `ncfpdf(x,df1,df2,ncf)` 生成非中心F分布的随机数。 - `gaminv(p,alpha,beta)` 计算伽马分布的逆累积分布函数，`p` 是累积概率，`alpha` 和 `beta` 是参数。 - `gampdf(x,alpha,beta)` 计算伽马分布的密度函数。 - `nbinpdf(x,r,p)` 计算负二项分布的密度函数，`r` 是成功次数，`p` 是单次试验的成功概率。 - `lognpdf(x,mu,sigma)` 生成对数正态分布的随机数，`mu` 和 `sigma` 分别是对数均值和对数标准差。 - `raylpdf(x,lambda)` 计算瑞利分布的密度函数，`lambda` 是尺度参数。 - `poisspdf(x,lam)` 用于计算泊松分布的密度函数，`lam` 是期望值。 - `weibpdf(x,k,scale)` 生成威布尔分布的随机数，`k` 是形状参数，`scale` 是比例参数。 - `tpdf(x,df)` 计算t分布的密度函数，`df` 是自由度。 4. **随机信号的数字特征**： - 在MATLAB中，可以使用统计函数如 `var` 来计算高斯随机信号的方差，`mean` 来计算均值，`std` 来获取标准差，`skewness` 和 `kurtosis` 分别计算偏斜度和峰度，这些都可用于理解随机信号的统计特性。 通过以上工具和函数，我们可以模拟和分析各种随机信号，进而理解信号的性质、进行参数估计或测试统计假设。在实际应用中，这些知识对于数据分析、滤波器设计、系统仿真和故障诊断等至关重要。