没有合适的资源?快使用搜索试试~ 我知道了~
数据结构和算法题解-1000多页.pdf
需积分: 0 27 下载量 117 浏览量
2021-05-09
22:27:49
上传
评论 1
收藏 98.21MB PDF 举报
温馨提示
目前自己写了500多道算法题解,部分整理成PDF格式,目前有1000多页,大家可以免费下载学习
资源推荐
资源详情
资源评论

前言
大家好,我是博哥,连续3年多的时间坚持在微信公众号“数据结构和算法”中写算法题,截止
到目前已经在公众号上发布了500多道算法题。现在我把部分算法题整理成PDF的格式,这样方便
大家阅读,有的可能时间比较久了,这里没有全部列出来。
最初写的时候代码都是截图,没法复制,后来写的是可以复制的,等有时间了我在把代码全部整
理也会放到百度网盘中,和这个文档一起,大家可以下载运行,我目前使用的都是java语言,如
果想切换到其他语言,也可以对照代码进行修改。
当然学习的脚步不能停止,我还会继续在公众号上不断的输出各种算法题,欢迎大家阅读。如果
大家不小心把这个文档搞丢了也没关系,可以到我微信公众号中回复“pdf”即可获取下载地
址,我把文档放到了百度网盘上了。这个文档也会不停的更新,因为我公众号会不停的写算法
题,所以也会隔段时间同步到这个文档上,大家可以直接在我公众号中回复“pdf”获取最新的
文档即可。关于我微信公众号大家可以扫描下方二维码关注。如果觉得不错的,可以相互转发,
我们大家一起学习。感谢大家的支持。
V4.0
注意:文章之前都是图文结合的,后来有了
视频,视频没法在pdf中播放,如果想看视
频可以直接点击,会跳转到到我公众号中,
然后就可以观看了。
543,剑指 Offer-动态规划解礼物的最大价值
收录于话题
#剑指offer
33个
A person who won't read has no advantage over one
who can't read.
识字却不愿阅读的人,比文盲也好不到哪去。
问题描述
在 一 个 m* n 的 棋 盘 的 每 一 格 都 放 有 一 个 礼 物 , 每 个 礼 物 都 有 一 定 的 价 值 ( 价 值 大 于
0 ) 。 你可 以 从 棋 盘 的 左上 角开 始 拿 格 子 里 的 礼 物 , 并 每 次 向 右 或 者 向 下 移 动 一 格 、 直 到
到达 棋盘 的右 下角 。给 定 一个 棋盘 及 其上 面的 礼 物的 价值 , 请 计 算你 最 多能 拿 到 多少 价 值
的礼 物?
示例 1 :
输 入 :
[
[ 1 , 3 , 1 ] ,
[ 1 , 5 , 1 ] ,
[ 4 , 2 , 1 ]
]
输 出 : 1 2
解 释 : 路 径 1 → 3 → 5 → 2 → 1 可 以 拿 到 最 多 价 值 的 礼 物
提示 :
0 < g r i d . l e n g t h < = 2 0 0
0 < g r i d [ 0 ] . l e n g t h < = 2 0 0
动态规划解决
原创
博哥 今天数据结构和算法
这题 可以 参照 40 9 ,动 态 规划 求 不同 路 径, 第 4 09 题 让 求 的 是 有 多 少种 路 径 , 而 这 题 让 求
的是 所有 路径 中数 字和 最大 的值 。这 题很 容易 想到 的解 决方 式就 是动 态规 划。
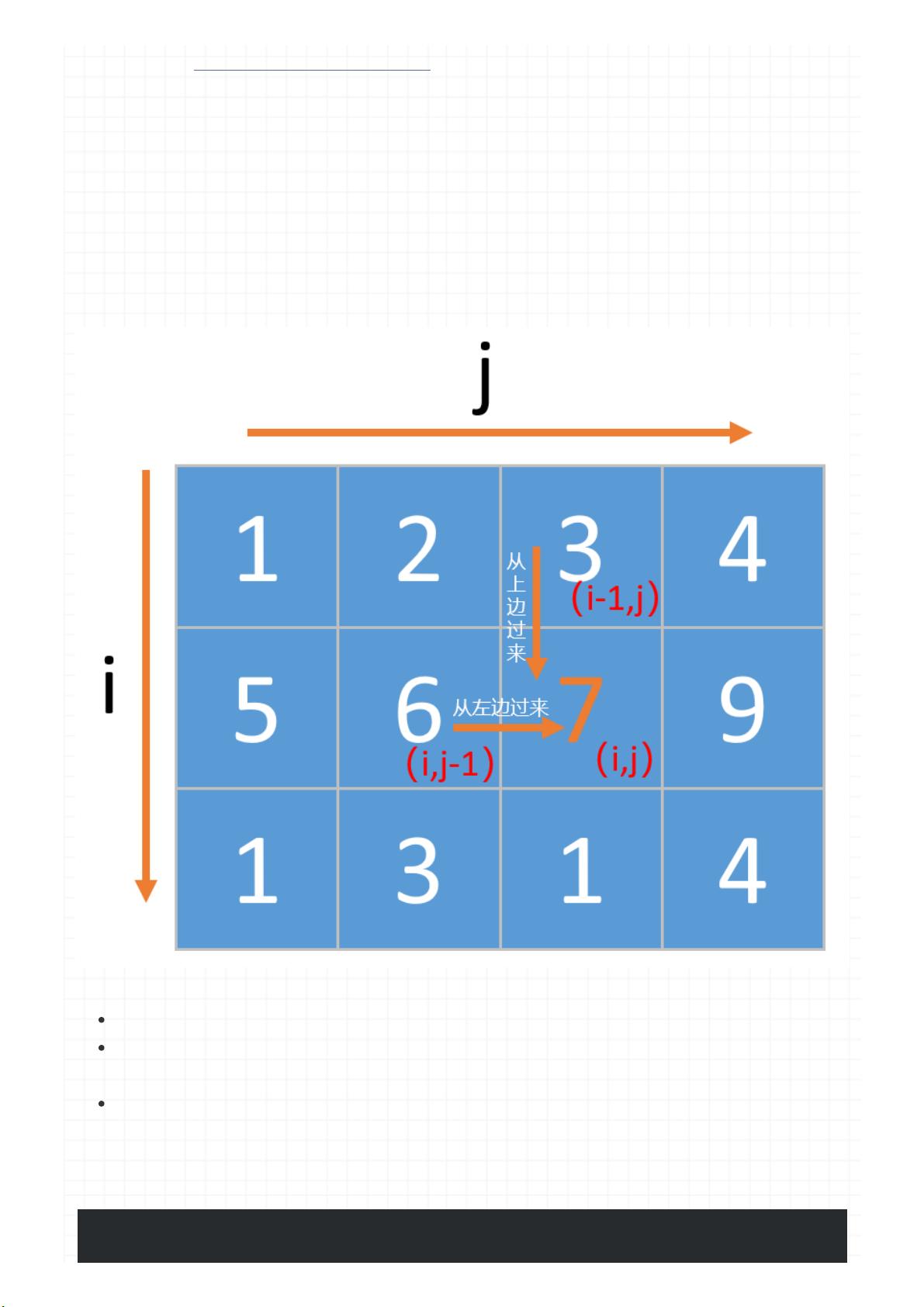
根 据 题 意 要 求 我 们 定 义 d p[ i] [j ] 表 示 从 矩 阵 的 左 上 角 走 到 坐 标 ( i , j ) 所 能 拿 到 的 最 大 礼
物。
如 果 要 走 到 坐 标 ( i , j ) , 我 们 可 以 从 坐 标 ( i -1 , j ) 往 下 走 一 步 , 或 者 从 坐 标 ( i , j -
1) 往右 走一 步, 到底 应该 从哪 里, 我们 应该 取这 两个 方向 的最 大值 ,所 以
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];
那么 边界 条件 是什 么呢
如果 在左 上角 ,d p[ 0] [0 ]= gr id [0 ][ 0] ,
如 果 在 最 上 边 一 行 , 因 为 不 能 从 上 面 走 过 来 , 只 能 从 左 边 走 过 来 , 所 以 当 前 值 是 他
左边 元素 的累 加。
如 果 在 最 左 边 一 列 , 因 为 不 能 从 左 边 走 过 来 , 只 能 从 上 边 走 过 来 , 所 以 当 前 值 是 他
上边 元素 的累 加。
来看 下代 码
1 public int maxValue(int[][] grid) {
2 //边界条件判断
3 if (grid == null || grid.length == 0)

3 if (grid null || grid.length 0)
4 return 0;
5 int m = grid.length;
6 int n = grid[0].length;
7 int[][] dp = new int[m][n];
8 dp[0][0] = grid[0][0];
9 //初始化dp的最上面一行,从左到右累加
10 for (int i = 1; i < n; i++) {
11 dp[0][i] = dp[0][i - 1] + grid[0][i];
12 }
13 //初始化dp的最左边一列,从上到下累加
14 for (int i = 1; i < m; i++) {
15 dp[i][0] = dp[i - 1][0] + grid[i][0];
16 }
17
18 //下面是递推公式的计算
19 for (int i = 1; i < m; i++) {
20 for (int j = 1; j < n; j++) {
21 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
22 }
23 }
24 return dp[m - 1][n - 1];
25 }
为 了 方 便 计 算 我 们 还 可 以 把 d p 的 宽 和 高 增 加 1 , 也 就 是 d p 的 最 上 面 一 行 和 最 左 边 一 列 不
存储 任何 数值 ,他 们都 是0 ,这 样是 为了 减少 一些 判断
1 public int maxValue(int[][] grid) {
2 if (grid == null || grid.length == 0)
3 return 0;
4 int m = grid.length;
5 int n = grid[0].length;
6 //为了方便计算,dp的宽和高都增加了1
7 int[][] dp = new int[m + 1][n+1];
8 //下面是递推公式的计算
9 for (int i = 0; i < m; i++) {
10 for (int j = 0; j < n; j++) {
11 dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]) + grid[i][j];
12 }
13 }
14 return dp[m][n];
15 }
动态规划代码优化
我们 来看 一下 这个 公式
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];
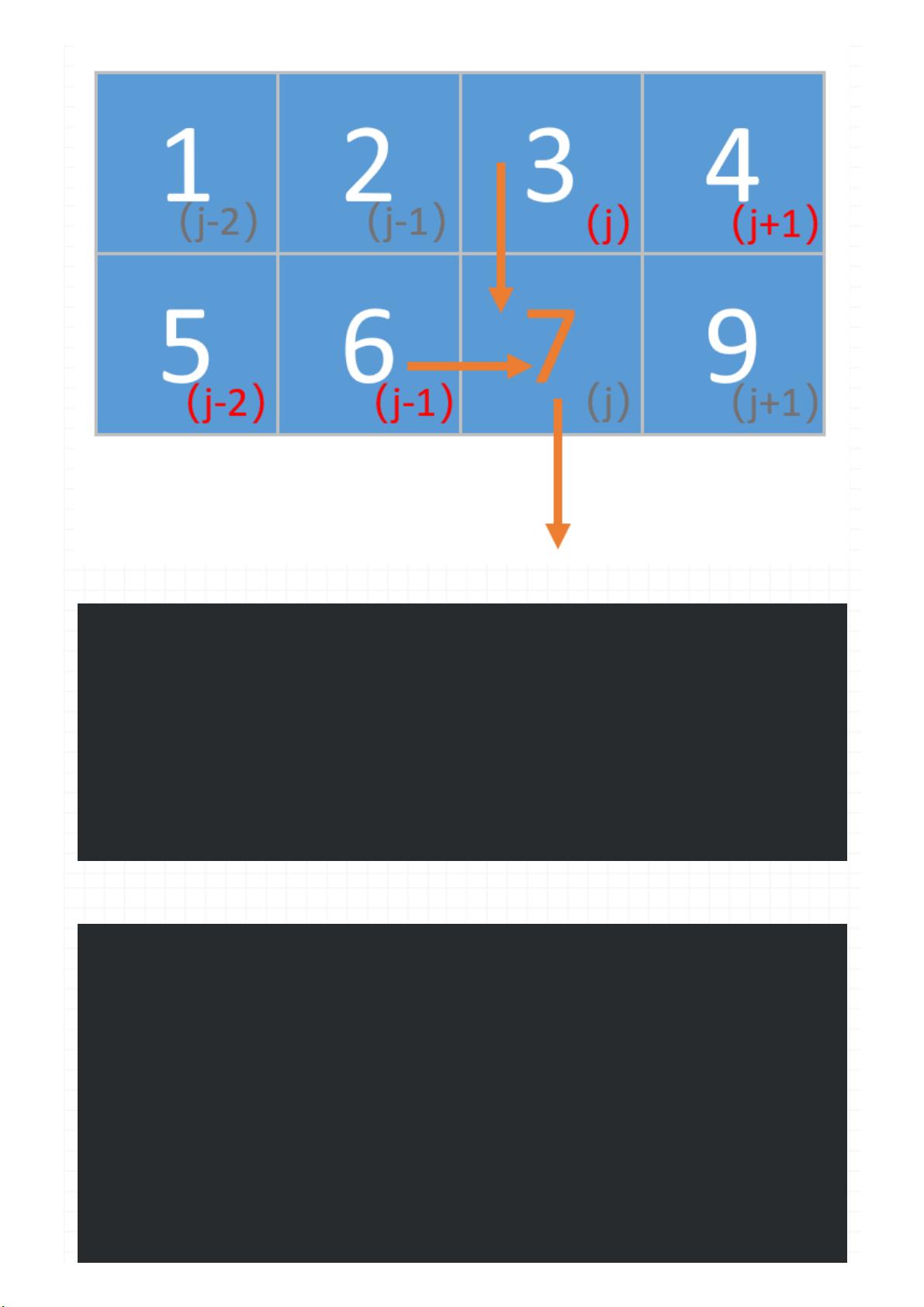
我 们 发 现 当 前 值 只 和 左 边 和 上 边 的 值 有 关 , 和 其 他 的 无 关 , 比 如 我 们 在 计 算 第 5 行 的 时
候 , 那 么 很 明 显 第 1 , 2 , 3 行 的 对 我 们 来 说 都 是 无 用 的 , 所 以 我 们 这 里 可 以 把 二 维 d p 改
成 一 维 的 , 其 中 d p [ i ] [ j - 1 ] 可 以 用 d p[ j- 1] 来 表 示 , 就 是 当 前 元 素 前 面 的 , d p[ i- 1] [j ] 可
以用 dp [j ]来 表示 ,就 是上 边的 元素 。
来看 下代 码
1 public int maxValue(int[][] grid) {
2 if (grid == null || grid.length == 0)
3 return 0;
4 int m = grid.length;
5 int n = grid[0].length;
6 //数组改成一维的
7 int[] dp = new int[n + 1];
8 for (int i = 0; i < m; i++) {
9 for (int j = 0; j < n; j++) {
10 dp[j + 1] = Math.max(dp[j], dp[j + 1]) + grid[i][j];
11 }
12 }
13 return dp[n];
14 }
我们 再 来仔 细 看 这 道题 , 题 中 没说 不 可以 修改 原 来数 组的 值 ,所 以我 还 可以 使用 题 中的 二
维数 组来 代替 二维 dp 数组
1 public int maxValue(int[][] grid) {
2 //边界条件判断
3 if (grid == null || grid.length == 0)
4 return 0;
5 int m = grid.length;
6 int n = grid[0].length;
7 //初始化dp的最上面一行,从左到右累加
8 for (int i = 1; i < n; i++) {
9 grid[0][i] += grid[0][i - 1];
10 }
11 //初始化dp的最左边一列,从上到下累加
12 for (int i = 1; i < m; i++) {
13 grid[i][0] += grid[i - 1][0];
14 }
15
16 //下面是递推公式的计算
17 for (int i = 1; i < m; i++) {
18 for (int j = 1; j < n; j++) {
19 grid[i][j] = Math.max(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
剩余1013页未读,继续阅读
资源评论

数据结构和算法
- 粉丝: 1w+
- 资源: 19
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 爱依克签批屏KY系列BS架构二次开发包,采用Websocket通信协议,内含驱动服务与开发文档,支持H5页面签名,PDF文件签名、指纹采集捺印以及摄像头拍摄和二代证身份身份信息读取
- Aspera高效文件传输产品技术解析与应用
- STM32DS3231硬件I2C读写,基于HAL库
- double数据做乘法保留两位小数的处理办法.txt
- 详细解读:毕业设计项目及写作技巧全程指南
- 学生成绩管理系统软件界面
- js判断时间多久之前.txt
- Temporal注解的作用.txt
- 五行与商业:古代智慧的探索与传承.docx
- 04747《Java语言程序设计(一)》真题试题 2019 -2021
- 处理苹果手机倒计时功能异常.txt
- HarmonyOS-ArkTS语言-购物商城的实现
- 导出表格报错net.sf.excelutils.ExcelException.txt
- 判断对象不为空的方法参考.txt
- Python爬虫技术入门与实战指南
- C++程序设计 课件PPT
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功