-201-
第十章 数据的统计描述和分析
数理统计研究的对象是受随机因素影响的数据,以下数理统计就简称统计,统计是
以概率论为基础的一门应用学科。
数据样本少则几个,多则成千上万,人们希望能用少数几个包含其最多相关信息的
数值来体现数据样本总体的规律。描述性统计就是搜集、整理、加工和分析统计数据,
使之系统化、条理化,以显示出数据资料的趋势、特征和数量关系。它是统计推断的基
础,实用性较强,在统计工作中经常使用。
面对一批数据如何进行描述与分析,需要掌握参数估计和假设检验这两个数理统计
的最基本方法。
我们将用 Matlab 的统计工具箱(Statistics Toolbox)来实现数据的统计描述和分析。
§1 统计的基本概念
1.1 总体和样本
总体是人们研究对象的全体,又称母体,如工厂一天生产的全部产品(按合格品及
废品分类),学校全体学生的身高。
总体中的每一个基本单位称为个体,个体的特征用一个变量(如
x
)来表示,如一
件产品是合格品记
0=x ,是废品记 1
=
x ;一个身高 170(cm)的学生记 170=x 。
从总体中随机产生的若干个个体的集合称为样本,或子样,如
n 件产品,100 名学
生的身高,或者一根轴直径的 10 次测量。实际上这就是从总体中随机取得的一批数据,
不妨记作
n
xxx ,,,
21
L , n 称为样本容量。
简单地说,统计的任务是由样本推断总体。
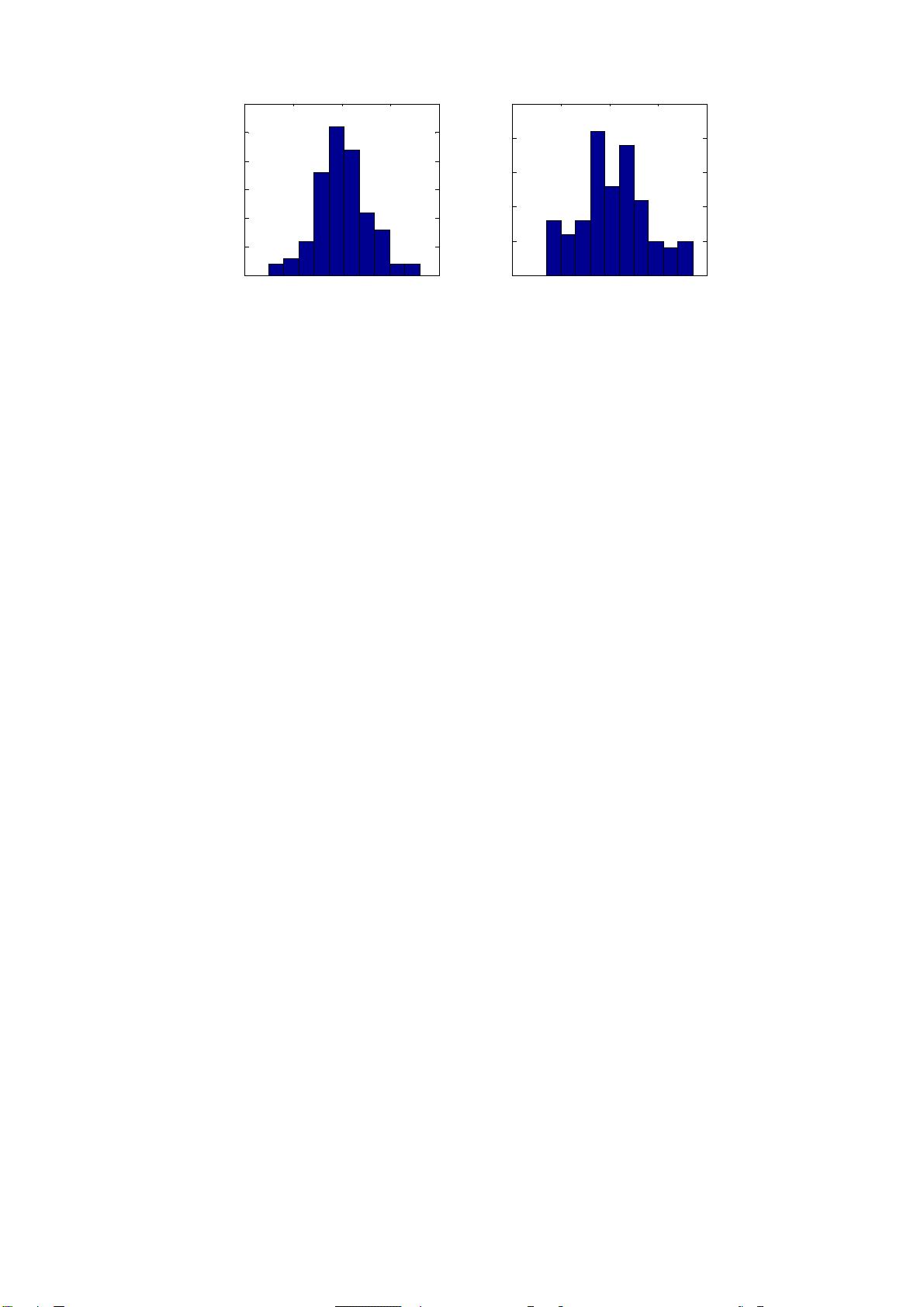
1.2 频数表和直方图
一组数据(样本)往往是杂乱无章的,做出它的频数表和直方图,可以看作是对这
组数据的一个初步整理和直观描述。
将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次
数,称为频数,由此得到一个频数表。以数据的取值为横坐标,频数为纵坐标,画出一
个阶梯形的图,称为直方图,或频数分布图。
若样本容量不大,能够手工做出频数表和直方图,当样本容量较大时则可以借助
Matlab 这样的软件了。让我们以下面的例子为例,介绍频数表和直方图的作法。
例 1 学生的身高和体重
学校随机抽取 100 名学生,测量他们的身高和体重,所得数据如表
表 1 身高体重数据
身高 体重 身高 体重 身高 体重 身高 体重 身高 体重
172 75 169 55 169 64 171 65 167 47
171 62 168 67 165 52 169 62 168 65
166 62 168 65 164 59 170 58 165 64
160 55 175 67 173 74 172 64 168 57
155 57 176 64 172 69 169 58 176 57
173 58 168 50 169 52 167 72 170 57
166 55 161 49 173 57 175 76 158 51
170 63 169 63 173 61 164 59 165 62
167 53 171 61 166 70 166 63 172 53
173 60 178 64 163 57 169 54 169 66
178 60 177 66 170 56 167 54 169 58
173 73 170 58 160 65 179 62 172 50
163 47 173 67 165 58 176 63 162 52