详解快速傅里叶变换FFT算法

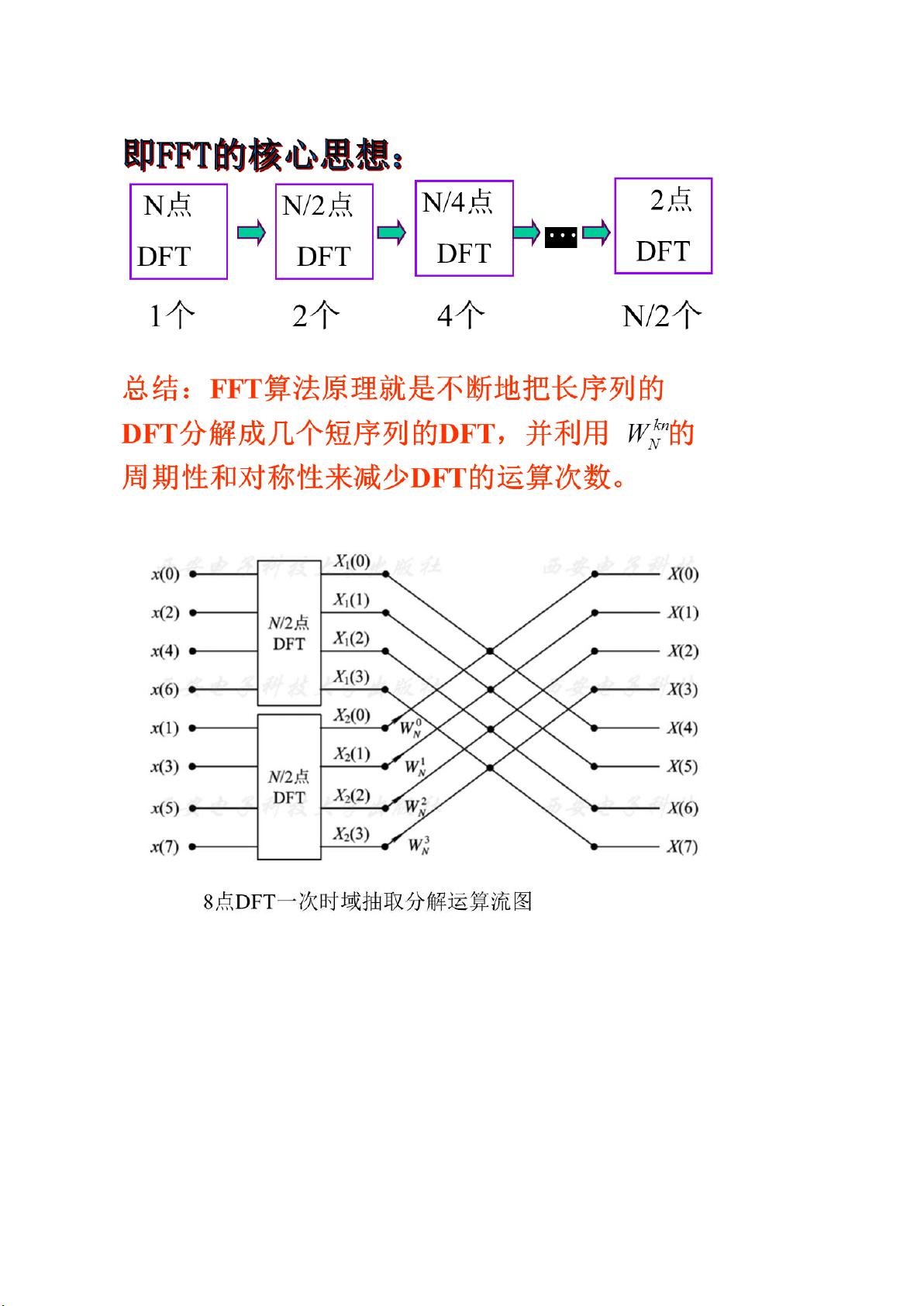
快速傅里叶变换（Fast Fourier Transform，FFT）是一种高效计算离散傅里叶变换（Discrete Fourier Transform，DFT）及其逆变换的算法。DFT是一种将时域离散信号转换为频域的数学方法，其在数字信号处理、图像处理、通信系统等领域中应用广泛。然而，传统的DFT算法运算复杂度高，当处理的样本数量N较大时，所需的计算量将非常巨大。因此，FFT算法的发明极大提高了DFT的计算效率，使其能够在现实中有实际应用的意义。 FFT算法是基于DFT的数学性质进行优化，其核心思想是利用周期性、对称性和可约性等数学特性，将复杂度从O(N^2)降低至O(NlogN)。这里我们详细解读FFT算法的工作原理。 DFT的定义如下： \[X(k)=\sum_{n=0}^{N-1}x(n)W_{N}^{nk}\] 其中，\(X(k)\)为频域表示，\(x(n)\)为时域信号，\(W_{N}^{nk}=e^{-j\frac{2\pi}{N}nk}\)为旋转因子，\(k=0,1,...,N-1\)。 DFT运算量的计算： - 对于每一个\(X(k)\)值的计算，需要\(N\)次复数乘法和\(N-1\)次复数加法，因此\(N\)个\(X(k)\)点的总运算次数为\(N^2\)次复数乘法和\(N(N-1)\)次复数加法。 - 将复数运算转换为实数运算，每次复数乘法需要4次实数乘法和2次实数加法，每次复数加法需要2次实数加法。因此，计算所有\(X(k)\)值需要\(4N^2\)次实数乘法和\(2N(N-1)\)次实数加法。 FFT算法减少了计算量，主要是通过将长序列的DFT分解为较短序列的DFT计算，然后通过组合这些短序列的DFT结果来得到原始序列的DFT。这种分解和组合的过程可以递归进行。 举例来说，对于点数\(N=2^m\)（\(m\)为整数），FFT算法可以将一个\(N\)点的DFT拆分成两个\(N/2\)点的DFT，再将\(N/2\)点的DFT拆分成两个\(N/4\)点的DFT，以此类推，直至拆分成两个点的DFT。这样的拆分和组合过程可以使用蝶形图（butterfly diagram）表示。 在蝶形运算中，每个蝶形节点涉及到一次复数乘法和两次复数加减法。通过递归地应用蝶形运算，最终的FFT算法的运算量大约是\(NlogN\)。对于\(N=1024\)的例子，原本需要计算一百多万次复数乘法，而在FFT算法下，复杂度降低到约一万次，大大提升了计算效率。 通过上面描述的步骤，FFT算法利用了DFT系数的固有特性简化了计算过程，将大量冗余的计算合并或省略，从而达到了降低运算量的目的。FFT算法按时间抽选（Decimation-In-Time, DIT）和频率抽选（Decimation-In-Frequency, DIF）两种方式，其中最常见的是库利-图基（Cooley-Tukey）算法。 在库利-图基FFT算法中，序列首先按点的奇偶性分为两组，再利用旋转因子的周期性和对称性来简化DFT的计算。通过蝶形运算的组合，得到原序列的DFT。 总结来说，FFT算法通过分解和合并的操作，利用数学上的周期性和对称性原理，将原问题的规模降低，并通过递归或迭代的方式，大幅度减少了计算次数，从而实现了在实际应用中对信号进行快速傅里叶变换的目的。FFT算法的成功使得频谱分析、信号处理等领域的实时性得到了显著提高，并在计算机科学与工程实践中发挥了巨大作用。