队列也是一种特殊的线性表

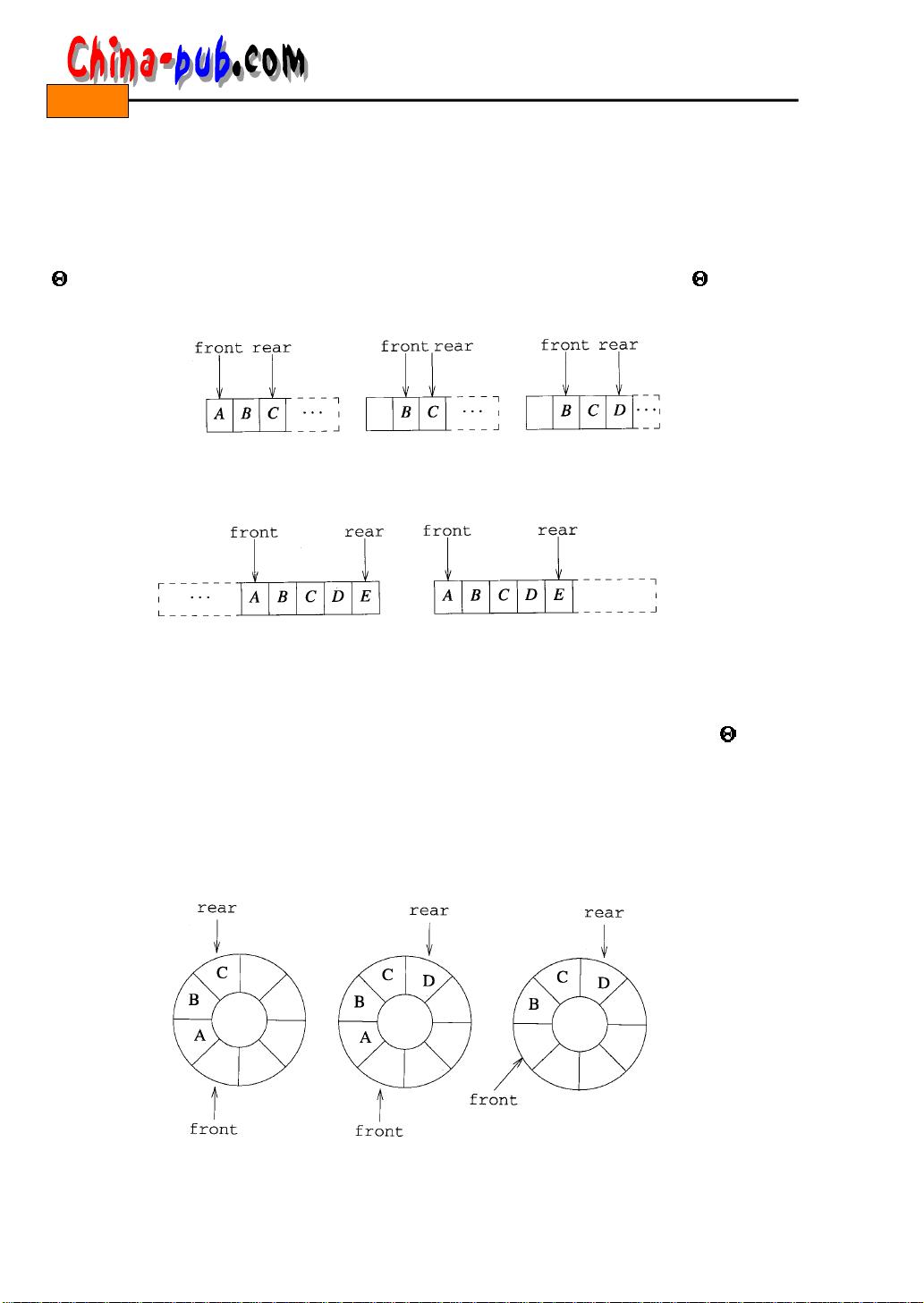
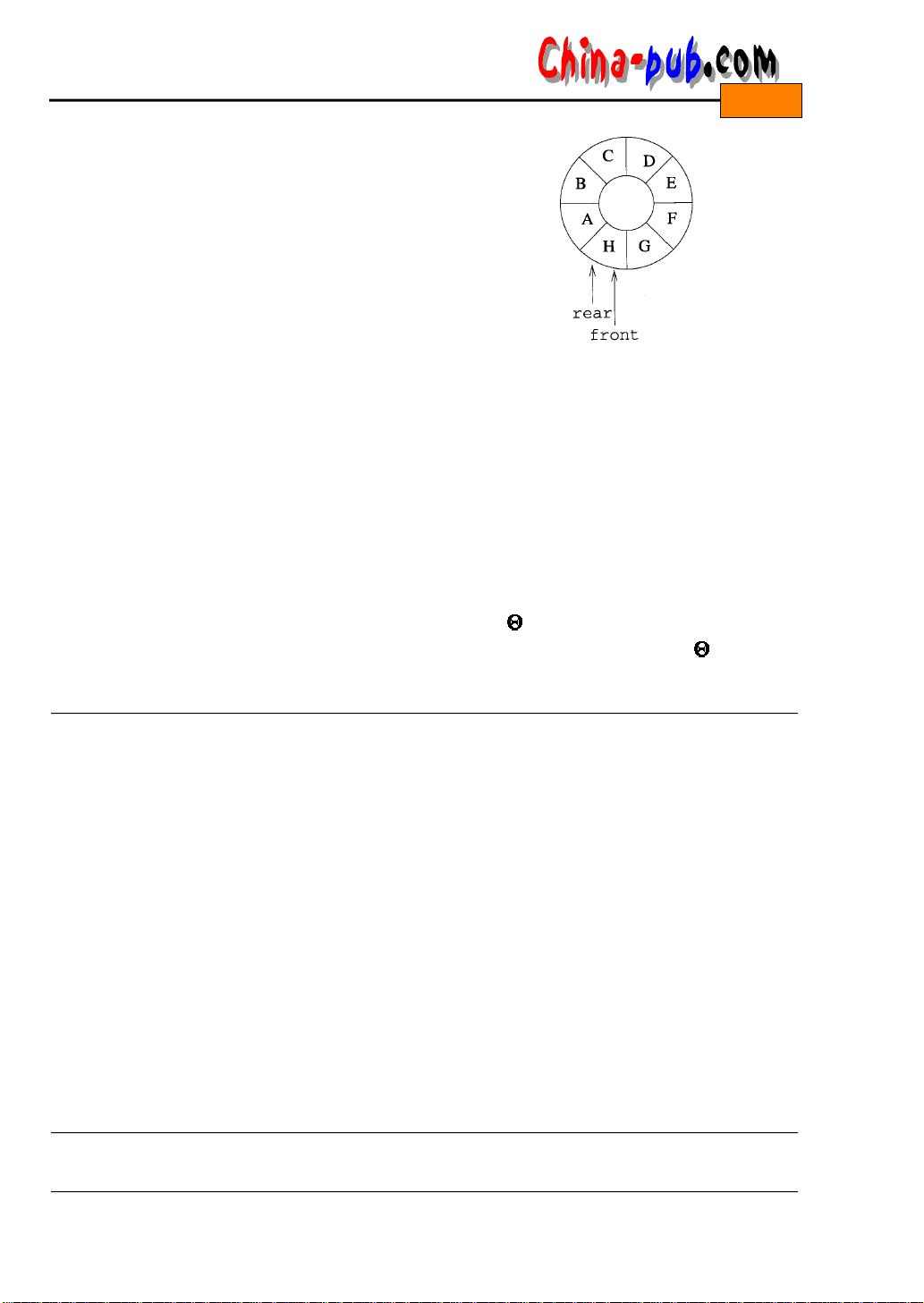
在本章的应用部分，给出了四个使用队列的应用。第一个应用是关于5 . 5 . 3节所介绍的火车 车厢重排问题。在本章中对这个问题做了修改，要求缓冲铁轨按F I F O方式而不是L I F O方式工 作；第二个应用是关于寻找两个给定点之间最短路径的问题，这是一个经典的问题。可以把这 个应用看成是5 . 5 . 6节迷宫问题的一种变化，即寻找从迷宫入口到迷宫出口的最短路径。5 . 5 . 6节 中的代码并不能保证得到一条最短的路径... ### 队列作为一种特殊的线性表 #### 一、队列的概念与特性 队列是一种特殊的线性表，它的主要特点是遵循先进先出（First-In-First-Out, FIFO）的原则，即最先加入队列的元素最先离开队列。与一般的线性表不同的是，队列的操作通常限制在两端进行：在队尾进行插入操作，在队首进行删除操作。 #### 二、队列的抽象数据类型描述 队列的抽象数据类型（Abstract Data Type, ADT）定义了一个队列的基本属性和操作方法： - **实例**：有序线性表，一端称为队首(front)，另一端称为队尾(rear)。 - **操作**： - `Create()`：创建一个空的队列。 - `IsEmpty()`：如果队列为空，则返回`true`，否则返回`false`。 - `IsFull()`：如果队列满，则返回`true`；否则返回`false`。 - `First()`：返回队列的第一个元素。 - `Last()`：返回队列的最后一个元素。 - `Add(x)`：向队列中添加元素`x`。 - `Delete()`：删除队首元素。 #### 三、队列的应用案例 队列在实际应用中有着广泛的应用场景。本章提到了几个具体的例子： 1. **火车车厢重排问题**：原本的问题是在5.5.3节中提到的，要求缓冲铁轨按照后进先出（Last-In-First-Out, LIFO）的方式工作。在本章中，该问题被修改为要求缓冲铁轨按照先进先出(FIFO)的方式工作，这就需要使用队列这种数据结构。 2. **寻找最短路径问题**：这是一个经典问题，可以看作是5.5.6节迷宫问题的一个变种。目标是从给定的起点到终点找到最短路径。虽然5.5.6节的代码可以找到一条路径，但不能保证是最短路径，而使用队列可以有效地解决这个问题。 3. **计算机视觉领域的图元识别**：在计算机视觉领域，队列可用于识别图像中的基本图形元素。通过队列来跟踪图像处理过程中的关键节点，有助于提高算法的准确性和效率。 4. **工厂仿真程序**：在一个包含多台机器的工厂中，每台机器负责不同的工序。通过建立一个模拟程序来追踪工厂中的任务流程，可以评估每项任务的总等待时间和每台机器的总等待时间，进而优化工厂布局。 #### 四、队列的数据结构实现 在实现队列的数据结构时，本章讨论了两种方法：公式化描述和链表描述。 1. **公式化描述**：使用公式(6-1)和公式(6-2)来描述队列。 - 公式(6-1): `location(i)=i-1` - 这个公式在堆栈中表现良好，但对于队列的删除操作，需要移动所有元素，时间复杂度为O(n)。 - 公式(6-2): `location(i)=location(1)+i-1` - 使用这个公式，删除操作只需要更新`location(1)`，时间复杂度降为O(1)。 2. **链表描述**：另一种实现队列的方法是使用链表。链表的优点在于插入和删除操作的时间复杂度都是O(1)，特别适合于实现队列。 通过上述分析可以看出，队列作为一种重要的数据结构，在多种应用场景下都有着独特的优势。无论是简单的火车车厢重排问题还是复杂的工厂仿真系统，队列都能够提供高效且灵活的解决方案。