Modelingandsimulationofaerialrefuelingbyfiniteelementmethod.pdf资源-CSDN文库

空中加油

ScienceDirect

需积分: 9 60 浏览量 2019-12-04 11:31:44 上传评论收藏 656KB PDF 举报

资源推荐

资源详情

资源评论

Modeling and simulation of aerial refueling by ﬁnite

element method

Z.H. Zhu

, S.A. Meguid

Department of Earth and Space Science and Engineering, York University, 4700 Keele Street, Toronto, Ont., Canada M3J 1P3

Engineering Mechanics and Design Laboratory, Department of Mechanical and Industrial Engineering,

University of Toronto, 5 King’s College Road, Toronto, Ont., Canada M5S 7G8

Received 6 February 2007; received in revised form 21 May 2007

Available online 8 June 2007

Abstract

The aerial refueling hose-and-drogue system is a special case of a generalized aerial cable towed system. The present

work investigates the eﬀect of pertinent parameters such as the cable tension, tow point disturbance and vortex wake

on the dynamic behavior and stability of the generalized model by using the ﬁnite element method with an accurate

and computationally eﬃcient three-noded, curved beam element. The analysis results show that the conventional modal

and spectrum analysis method is inappropriate for the dynamic stability analysis of the aerial cable towed system. This

is because the mechanism of instability due to the tow point disturbance is not the resonance of the aerial cable towed

system but the wave propagation downstream along the cable absorbing energy from the airﬂow when the wave propaga-

tion speed is less than the airﬂow speed. The study also demonstrates that the vortex wake has a signiﬁcant impact on the

dynamics of the aerial cable towed system. The short cable system will orbit with the vortex and the orbiting behavior will

diminish as the cable length increases.

Keywords: Aerial refueling; Finite element method; Curved beam; Dynamic modeling; Simulation

1. Introduction

By far the most common method for in-ﬂight refueling is the probe-and-drogue system, in which a tanker

aircraft deploys a hose behind it with a drogue on the end of the hose (a meshwork cone whose drag keeps the

hose in a stable position). A receiving aircraft approaches the drogue with a probe, which is inser ted into the

drogue to link the fuel systems. It is reported that the hose-and-drogue system suﬀered a 2.5% failure rate in

operation (Gates and McCarthy, 2000). Most of the incidents occur when the hose becomes slack and loses the

stabilizing eﬀect of hose tension due to: (i) a malfunction of the hose reel mechanism failing to take up the

slacking hose, (ii) unstable motion of the tanker, (iii) vortex induced wake behind the tanker, and (iv) poor

design of the drogue, to name just a few. As a result, the hose becomes unstable, high tension spikes are gen-

doi:10.1016/j.ijsolstr.2007.05.026

Corresponding author. Tel.:+ 1 416 736 2100x77729; fax: +1 416 736 5817.

E-mail address: gzhu@yorku.ca (Z.H. Zhu).

Available online at www.sciencedirect.com

International Journal of Solids and Structures 44 (2007) 8057–8073

www.elsevier.com/locate/ijsolstr

erated in the hose and ultimately the drogue will be ruptured from the hose (Vassberg et al., 2002, 2004, 2005 ).

These accidents motivate the current study to characterize the dynamics of the aerial hose-and-drogue refu-

eling system in order to improve the safety of aerial refueling operation and potentiall y save lives and costs

related to the accidents and damages.

2. Statement of problem

2.1. Generalized model of aerial refueling hose and drogue

The aerial refueling hose-and-drogue system consists of three sub -systems: (i) the hose handling system, (ii)

the hose, and (iii) the drogue. A generalized model of the system can be derived by rationalizing the charac-

teristics of each sub-system. First, the handling system is a hydraulically controlled winch system inside a pod

that is mounted on a tanker aircraft. The pod stores, deploys and controls the positions of refueling hose and

drogue relative to the probe of a receiving aircraft by either reeling-in or paying-out the hose in response to the

variation of hose tension. The motion of a pod consists of the global rigid-body movement and the local struc-

tural deformation of the tanker. Because the mass and the size of a tanker are generally several orders higher

in magnitude than the hose and drogue, it is reasonably assumed that the motion of a pod is independent of

the motion of the hose and the drogue. Therefore, the handling system can be ideal ized as a tow point with a

prescribed motion. Second, the hose transfers fuels from the tanker to the receiver and serves as a tension

member to tow the drogue. It usually has a very large ratio of length over diameter. For instance, the ratio

of a typical refueling hose is over 350 (Vassberg et al., 2002). Therefore, the hose can be idealized as an elastic

cable subjected to the primary environmental eﬀects such as the free stream velocity and the vo rtex wake gen-

erated by the tanker aircraft. Finally, the drogue is a ﬁtting attached to the end of the hose to provide (i) a

coupling point with the receiving aircraft’s probe , and (ii) a suﬃcient drag to stabilize the hose. Considering

the ratio of the hose length over the drogue’s dimension, the drogue can be reasonably simpliﬁed as a lumped

point mass called towed body. Thus, the aerial refueling hose-and-drogue system can be idealized as a general-

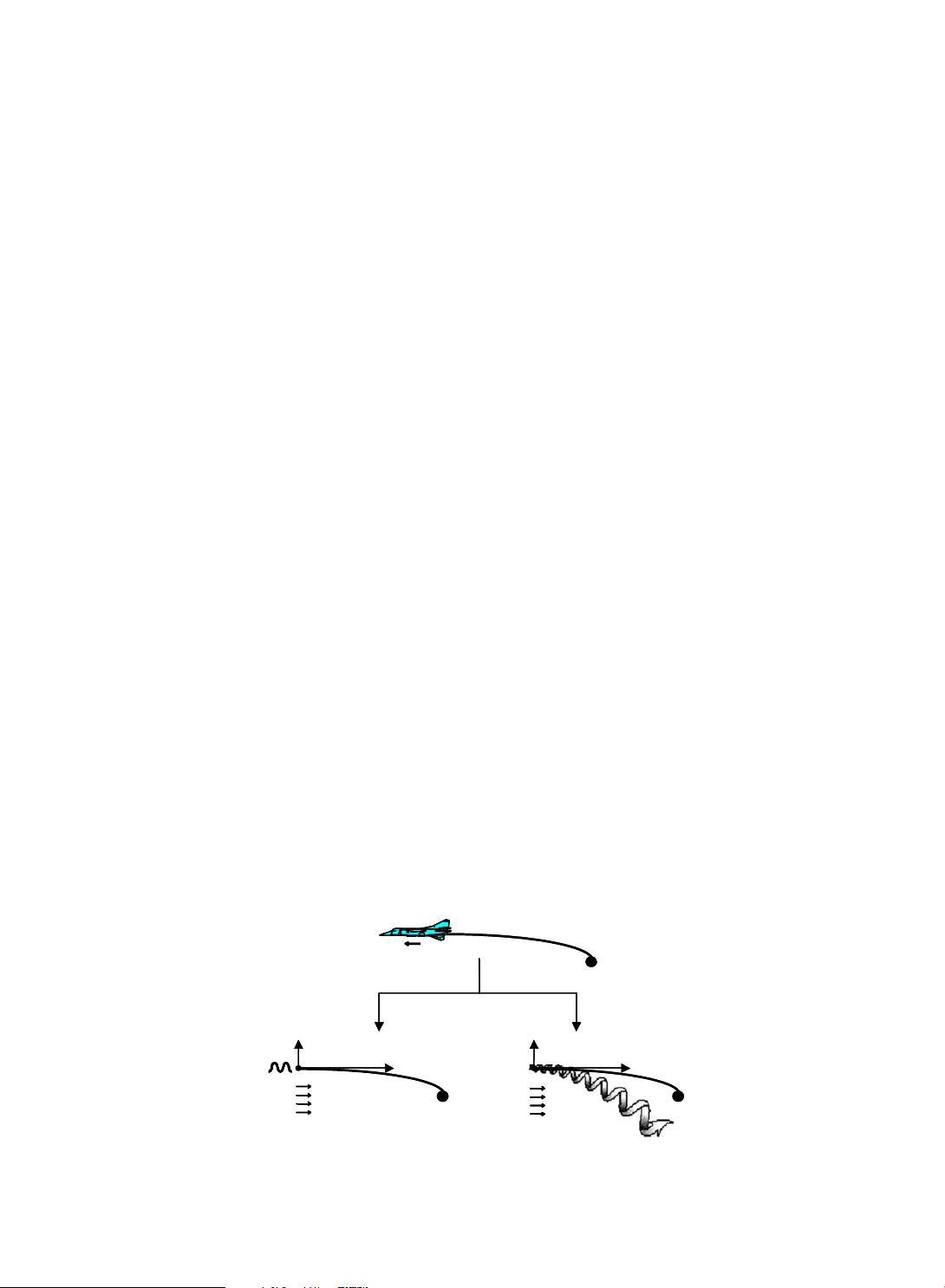
ized aerial cable towed system with a prescribed motion at the tow point, as illustr ated in Fig. 1. Based upon

the ab ove reasoning, the pertinent parameters for the dynamics of an aerial cable towed system can be out-

lined as the followings:

(i) drag, weight and mechanical properties of the cable,

(ii) drag and weight of the towed body,

(iii) prescribed motion at the tow point,

(iv) disturbance at the towed body due to the coupling between the drogue and the probe, and

(v) vortex wake behind the tanker aircraft.

(t)

Physical Model

Disturbance from tow point Disturbance from wake

Idealization

Fig. 1. Idealization for generalized model of aerial cable towed system.

8058 Z.H. Zhu, S.A. Meguid / International Journal of Solids and Structures 44 (2007) 8057–8073

2.2. Existing treatments of aerial cable towed system

A general cable system may be divided into two main groups: the low tension cable systems and the high

tension cable systems depending on whether the cable i s used for load bearing or not. The aerial refueling

system uses the hose to transfer fuels from one aircraft to another and can be classiﬁed as a low tension

cable system. The term of ‘‘low tension cable’’ refers to a class of cable systems in which a cable i s subjected

to a very small and/or dynamically ﬂuctuating tension that may vanish anywhere along the cable length. A

comprehensive body of knowledge exists in dealing with the taut cable dynamics (Etkin, 1998). However,

signiﬁcantly much less has been accomplished in the dynamic and stability analysis of the low tension cable

system, where the most of existing approaches simplify the cable as a tension member that cannot resist

compressive, bending and torsional loads. Unlike the highly tensioned cable where the cable tension is sev-

eral orders of magnitude higher than its bending and torsional moments, the fundamental mechanism of

energy propagation in a low tension cable is changed from the membrane dominant state to the bending

dominant state (Burgess, 1992; Howell, 1992). The classic cable theory provides inaccurate results in the

low tension region and suﬀers a singular problem when the cable tension disappears anywhere along the

cable. The limitations of the existing approaches have motivated the studies (Burgess, 1992; Howell,

1992; Koh et al., 1999; Buckham and Nahon, 1999; Zhu et al., 2001; Wu et al., 2003; Buckham et al.,

2004; Zhu and Meguid, 2006a,b) for alternative approaches to alleviate the singularity problem associated

with the classic cable theory by adding such eﬀects as artiﬁcial damping, higher order terms, and bending

stiﬀness of cable. For instance, Zhu et al. (2001) tried to avoid the singular problem by adding artiﬁcial

damping to their cable element in modeling the cable towed sonar system, where a resonant vibration of

the cable and sonar body may occur due to the random motion of the surface towing ship at low or zero

towing speed. Among all the alternative solutions, however, only the approach based o n the beam bending

theory is a natural extension of the classic cable theory and has a sound theoretical foundation and physical

meaning. Burgess (1992) and Howell (1992) modeled a low tension cable using a simpliﬁed 2D curved beam

theory for a n underwater cable system. Koh e t al. (1999) studied a free fall cable experimentally and numer-

ically using the same curved beam theory with ﬁnite diﬀerence method. Wu et al. (2003) studied the planar

vibration of a slacking cable using the Bernoulli beam theory. Buckham et al. (2004) proposed a 3D curved

cable element with bending and torsional stiﬀness specially designed for the marine application. Zhu and

Meguid (2006a,b) developed a generic 3D c urved beam element using Love’s curved beam theory to study

the dynamics of low tension cables and the coupling process of refueling hose and drogue. Special treatment

was developed in the new element to eliminate the membrane locking which is commonly associated with

the curved beam elements.

The modeling of the low tension cable system with a realist ic and robust description of cable dynamics inev-

itably leads to a complex mathematical problem and consequently requires numerical solution techniques. The

ﬁnite diﬀerence (FD) and the ﬁnite element (FE) methods are the most common numerical procedures used in

engineering analysis. The FD method approximates the governing equations of the cable by some diﬀerence

equations along its length. Solutions of the cable dynamics using FD are very popular and predominant in the

dynamic analysis of cable systems because of their mathematic simplicity; see the works of Buckham and

Nahon (1999) , Burgess (1992) and other researchers (Howell, 1992; Koh et al., 1999). However, the FD

method is problem speciﬁc and cannot be implemented in general-purpose analysis programs for complex

geometries with multiple cable branches or diﬀerent cable properties along the cable length. The FE method

is probably the most appealing technique among all numerical methods, although its mathematical formula-

tion processes are usually more complicated than FD method. However, the FE, once established, is capable

to handle the diﬀerent and complex cable syst ems in an algorithmic fashion without re-formulation, allowing

for its implementation in general-purpose analysis programs. Ther efore, the authors decided to employ the FE

method to model the generalized aerial cable towed system using beam theory.

There are many types of ﬂexible beam elements available in the literature for modeling the cable (Schreﬂer

and Odorizzi, 1983). The simplest one is the two-noded straight element. The straight element, however, vio-

lates the slope continuity condition of a slacking cable by discretizing the curved cable into straight segments.

As a result, excessive bending stiﬀness or membr ane locking becomes prevalent (Bucalem and Bathe, 1995).

Curved beam elements, which are based on the curvilinear strain ﬁeld description, have an advantage

Z.H. Zhu, S.A. Meguid / International Journal of Solids and Structures 44 (2007) 8057–8073 8059

剩余16页未读，继续阅读

评论收藏

内容反馈

RandStream

粉丝: 1
资源: 2

Modeling and simulation of aerial refueling by finite element me...

最新资源

Modeling and simulation of aerial refueling by finite element me...

Numerical simulation of laser-generated Lamb wave by finite element method in thin transversely isotropic laminate composite

finite element method (Zienkiewicz).pdf

A finite element simulation

The finite element method

finite element method

英文原版-Moving Finite Element Method 1st Edition

System Dynamics_ Modeling, Simulation, and Control of Mechatronic Systems

MODELING AND SIMULATION OF MECHATRONIC SYSTEMS.pdf

Modeling-and-Simulation-in-Python-pdf.pdf.pdf

Modeling and simulation of large-scale ductile fracture in plates and shells

Modeling and Simulation of Aerospace Vehicle Dynamics

AnalyticalSystemDynamicsModelingandSimulation-Analytical System Dynamics Modeling and Simulation.part2.rar

Finite Element Method in Machining Processes

vehicle dynamics modeling and simulation 车辆动力学建模与仿真

The Modeling and Simulation of Photovoltaic Cells.slx

按照文献做的光伏电池组件模型调试出错附老外文献-不错 MODELING AND SIMULATION BASED APPROACH OF.pdf

underwater acoustic modeling and simulation

Network Modeling and Simulation A Practical Perspective

Behavioral Modeling and Predistortion of Wideband Wireless Transmitters

(Modeling and Simulation in Science, Engineering and Technology

Digital Signal Integrity-Modeling and Simulation with Interconnects and Package

Tecnomatix Plant Simulation Modeling and ....pdf

Practical Finite ElementModeling in Earth Science Using Matlab

Dynamic System Biology and Modeling and Simulation

最新资源