### 5.2 谱系聚类法
#### 一、类间距离定义与计算方法
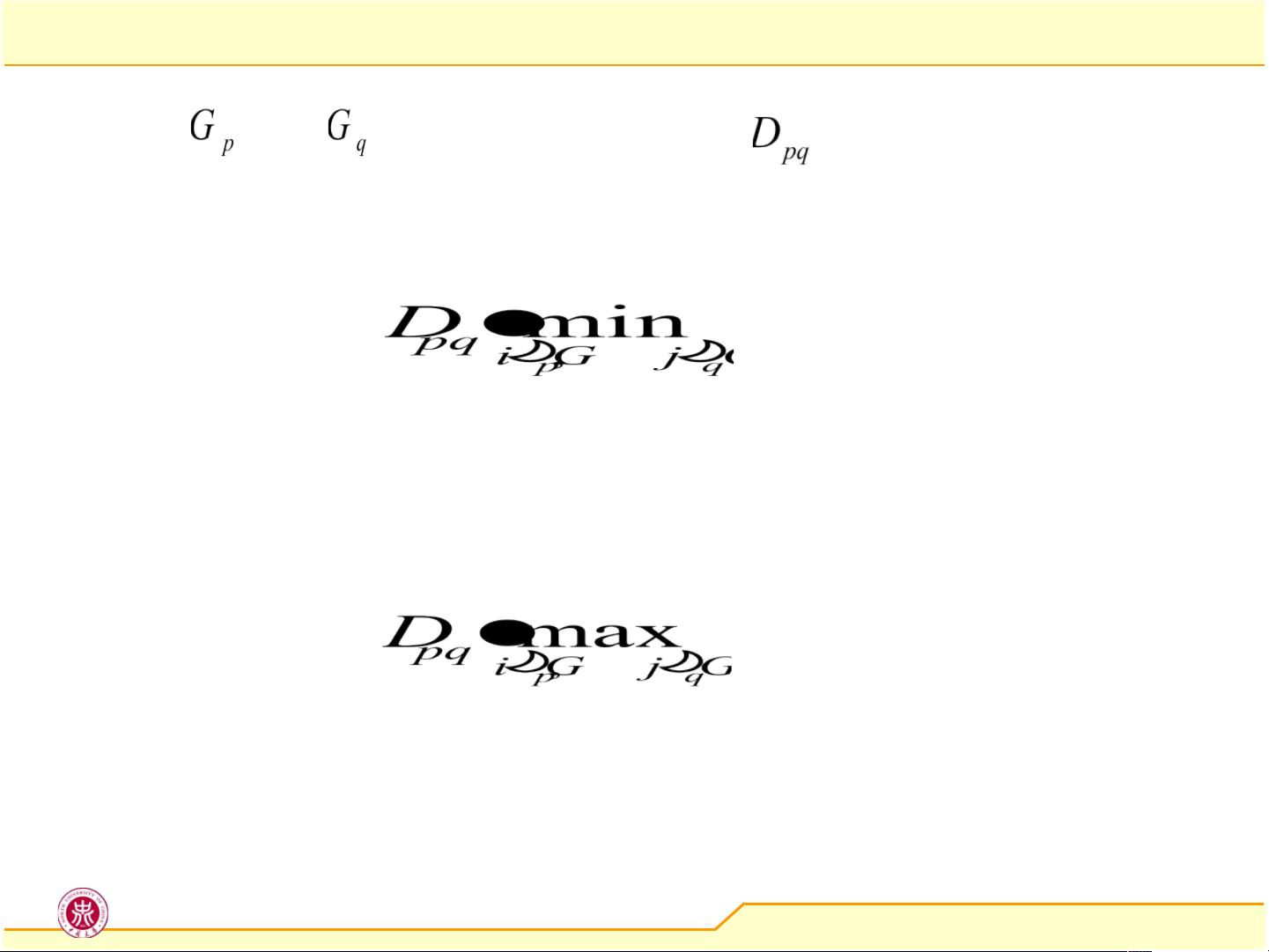
##### 1. 最短距离(Single Linkage)
最短距离法是谱系聚类中最基本的方法之一,它定义两个类之间的距离为这两类中任意两个样本之间距离的最小值。这种方法容易形成细长的簇,适用于捕捉复杂的数据分布。
##### 2. 最长距离(Complete Linkage)
最长距离法则考虑两个类中任意两个样本之间的最大距离,即取两个类间距离的最大值作为类间距离。这种方法倾向于形成球形簇,对于异常值较为敏感。
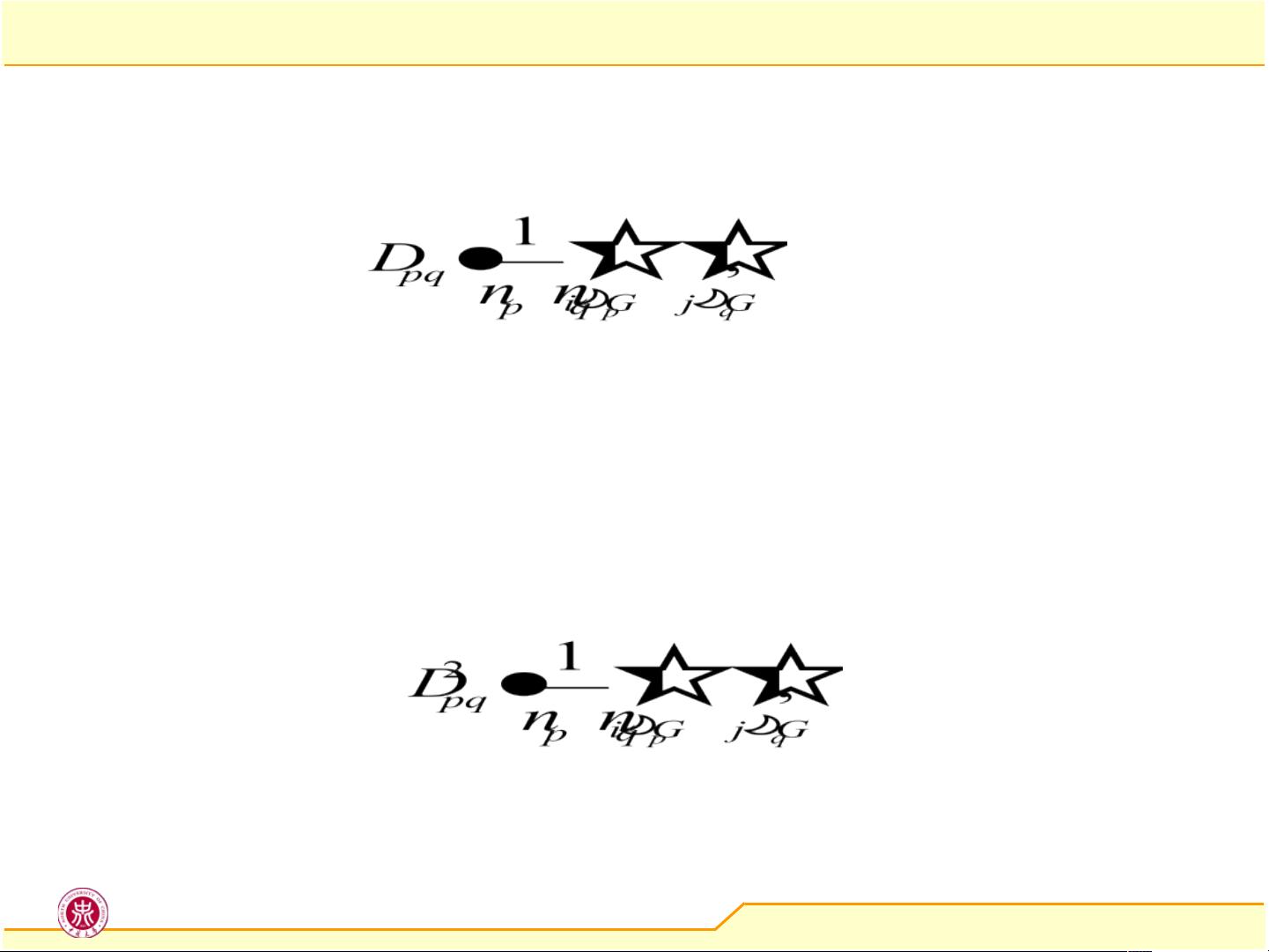
##### 3. 类平均距离(Average Linkage)
类平均距离是通过计算两个类中所有样本间的距离平均值来确定类间距离。这种方法介于最短距离和最长距离之间,既不太容易受异常值影响,也不易形成极端形状的簇。
##### 4. 重心距离(Centroid Method)
重心距离是根据两类的重心(均值向量)之间的距离来定义类间距离。重心是类中所有样本均值的几何中心点,这种方法能够较好地处理非球形簇。
##### 5. 离差平方和距离(Ward’s Method)
离差平方和距离考虑了合并后的簇内样本到簇中心的平方误差之和。该方法试图最小化簇内样本间的差异,适用于数据具有清晰边界的情况。
#### 二、类间距离的递推公式
递推公式是在聚类过程中逐步构建较大类时计算新类与其他已存在类间距离的方法。
##### 1. 最短距离的递推公式
如果两个类合并,新的类与其他类之间的最短距离可以通过原来两个类与其他类之间的最短距离来计算,即选择两个类与其他类之间所有可能组合中的最小值作为新类与该类之间的距离。
##### 2. 最长距离的递推公式
最长距离的递推公式与最短距离类似,但选取的是最大值。
##### 3. 类平均距离的递推公式
类平均距离的递推公式基于合并后的新类与旧类之间的所有可能的两两样本距离的平均值。
##### 4. 重心距离的递推公式
合并两个类形成新类后,新类的重心可通过原两个类的重心和各自的样本数量计算得出。新类与任一类的重心距离可直接由新类的重心与该类重心计算得出。
##### 5. 离差平方和距离的递推公式
对于离差平方和距离,合并两个类后,新的类与其他类之间的离差平方和距离可通过原两类与其他类之间的离差平方和距离以及原两类的样本数量计算得出。
#### 三、谱系聚类法的步骤
谱系聚类是一种自底向上的层次聚类方法,其步骤如下:
1. **初始化**:每个样本都作为一个单独的簇。
2. **距离矩阵构建**:计算所有样本间的距离,并构建距离矩阵。
3. **迭代合并**:
- 找到距离矩阵中最近的两个簇(通常是最小距离),将这两个簇合并为一个新簇。
- 更新距离矩阵:删除原两个簇对应的行和列,计算新簇与其他簇之间的距离,并将结果添加到距离矩阵中。
4. **重复迭代**:重复上述步骤,直到所有样本都被合并为一个簇。
#### 四、谱系聚类法的应用案例
以欧洲各国语言的相似性为例,通过测量每两种语言之间在数字1至10的第一个字母不同的个数来定义距离,可以使用谱系聚类法对这些语言进行聚类。
1. **最短距离法**:根据最短距离法进行聚类,得到的谱系图显示了哪些语言更相似。
2. **最长距离法**:同样地,使用最长距离法进行聚类,可以得到另一种聚类结果。
3. **类平均距离法**:类平均距离法的结果可能会更加平衡,因为它综合了所有样本之间的距离。
通过上述步骤和方法,我们可以有效地对数据进行层次聚类,进而发现数据内在的结构和模式。