立体几何证明题定理推论汇总.doc

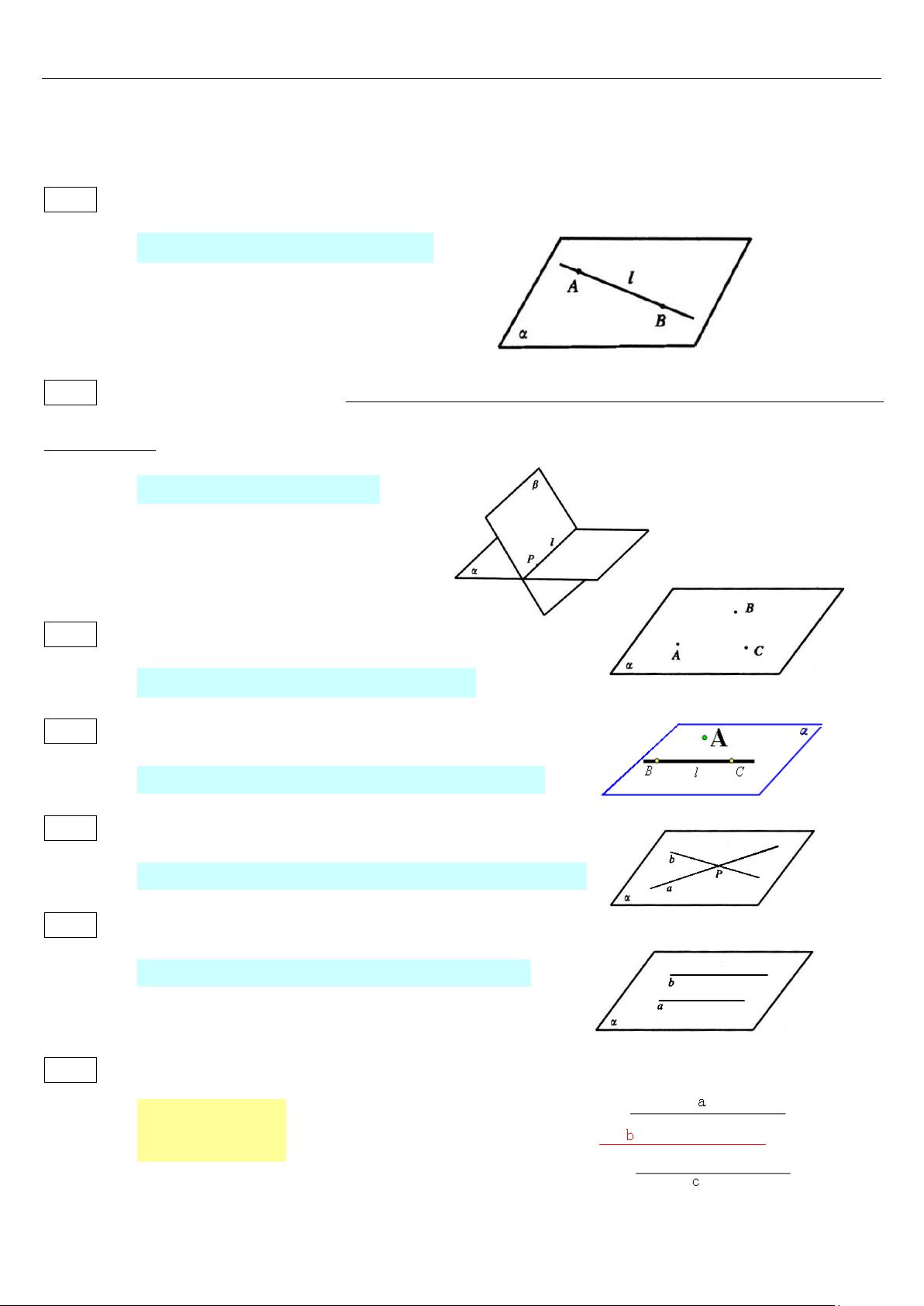
立体几何是数学中一个重要的分支，主要研究三维空间中的几何对象和它们之间的关系。这个文档“立体几何证明题定理推论汇总”整理了立体几何中的基本公理、定理和推论，对于理解和解决立体几何问题至关重要。下面将详细阐述其中的关键知识点。 我们来看三个基本的公理： 1. 公理1（直线在平面上）指出，如果一条直线上的两点在一个平面内，那么这条直线上所有点都在这个平面内。这表明平面可以无限延展，并且用来验证直线是否属于某个平面。 2. 公理2（相交平面）表明，如果有两个平面有一个公共点，那么它们之间存在一条通过这个公共点的唯一公共直线。这用于证明平面的相交关系以及多点共线的情况。 3. 公理3（三点定平面）表示，不在同一条直线上的三点可以唯一确定一个平面。这用于证明多点共面和多线共面的情况。 接着，公理3的推论包括： - 推论1（直线与直线外点定平面）：经过一条直线和这条直线外的一点，有且仅有一个平面。 - 推论2（相交直线定平面）：经过两条相交直线，有且仅有一个平面。 - 推论3（平行直线定平面）：经过两条平行直线，有且仅有一个平面。 公理4（平行公理）规定，平行于同一条直线的两条直线也互相平行。这在证明线线平行时非常关键。 在平行关系方面，有以下几个重要定理： - 线面平行的判定定理（2）：如果平面外的直线与平面内的直线平行，那么该直线与平面平行。 - 线面平行的性质定理（3）：如果一条直线与平面平行，那么通过这条直线的任何平面与原平面的交线与该直线平行。 - 面面平行的判定定理（4）：如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。 - 面面平行的判定（5）：如果两个平面都垂直于同一条直线，那么这两个平面平行。 - 面面平行的性质（6）：两个平行平面与第三个平面相交，其交线平行。 - 面面平行的性质（7、8、9）：平行平面内的直线互相平行，一条直线垂直于两个平行平面中的一个则垂直于另一个，以及两个平面平行于同一平面则彼此平行。 在垂直关系上，有三垂线定理（10、11）和线面垂直的判定与性质（12、13、14、15），它们描述了直线与平面或平面与平面的垂直关系，并提供了判断垂直性的方法。 这些公理、定理和推论构成了立体几何证明题的基础，帮助我们理解并解决涉及空间几何的各种问题。掌握这些知识点，对于学习立体几何和解决相关证明题至关重要。