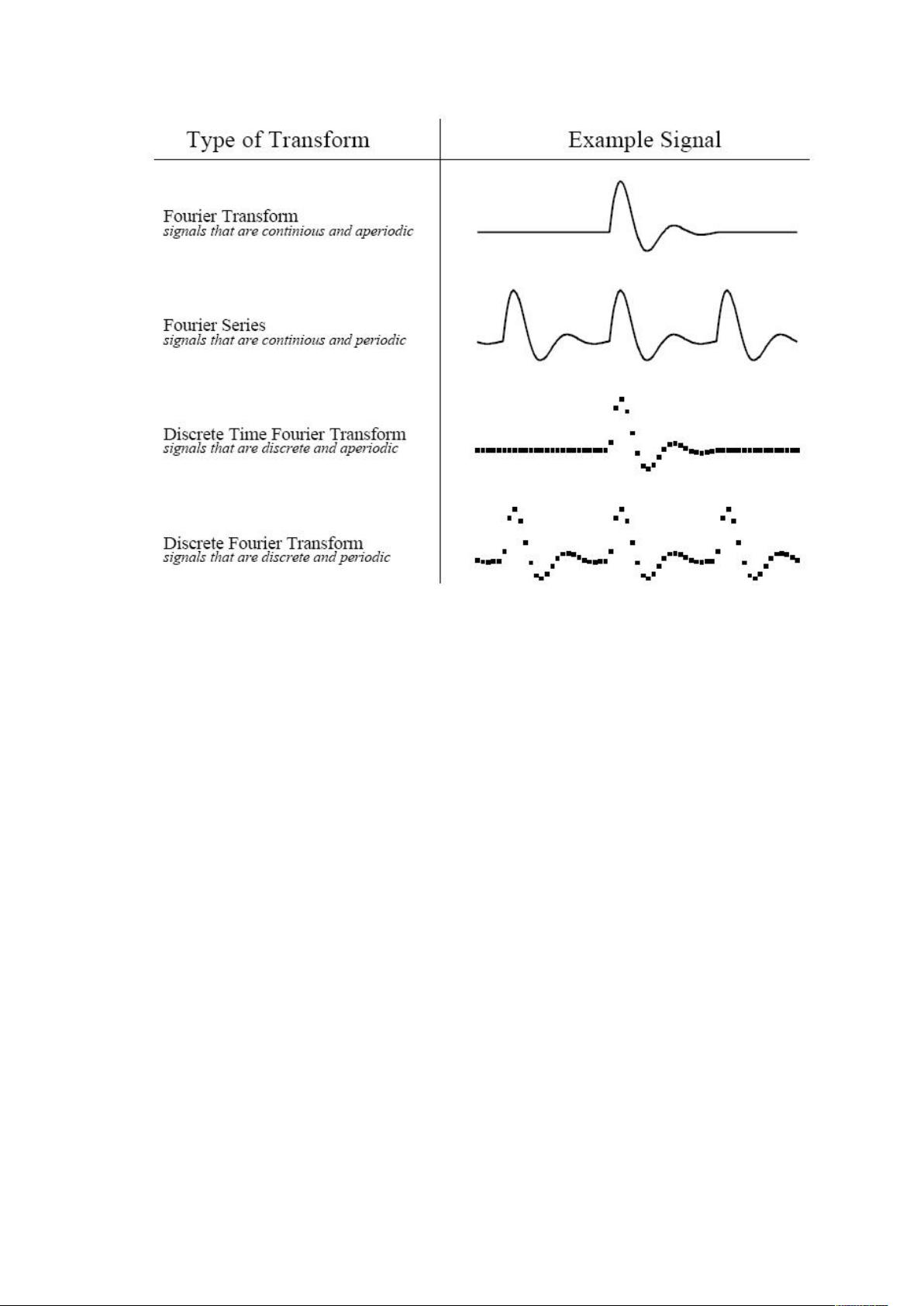
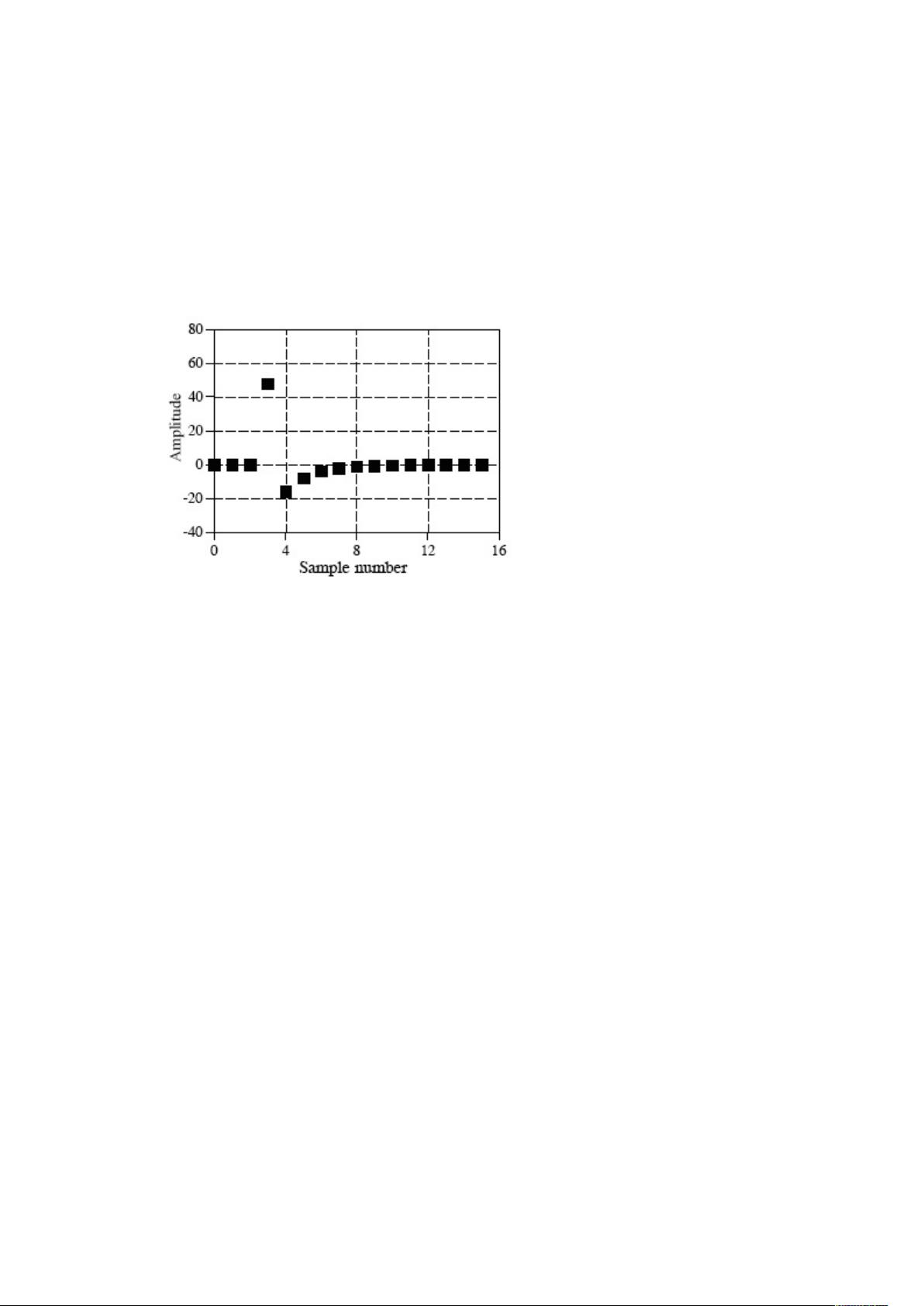
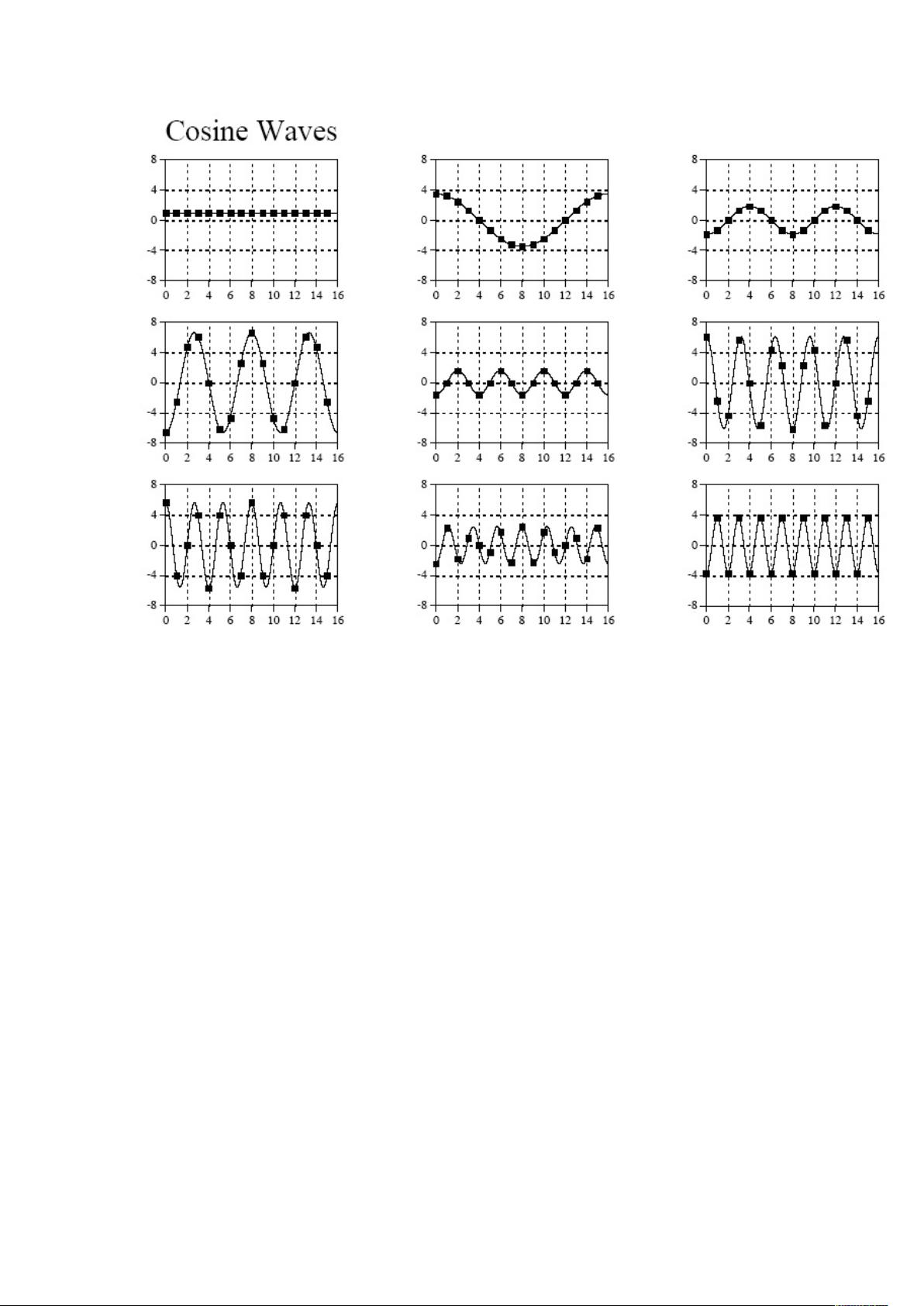
深刻理解傅里叶变换.pdf

深刻理解傅里叶变换 傅里叶变换是信号处理领域中的一种基本技术，它将信号从时域转换到频域，以便更好地分析和处理信号。傅里叶变换的提出可以追溯到十八世纪法国数学家和物理学家傅立叶（Jean Baptiste Joseph Fourier），他在1807年发表了一篇论文，论证了任何连续周期信号可以由一组适当的正弦曲线组合而成。 傅里叶变换的分类： 根据原信号的不同类型，傅立叶变换可以分为四种类别： 1. 非周期性连续信号傅立叶变换（Fourier Transform） 2. 周期性连续信号傅立叶级数（Fourier Series） 3. 非周期性离散信号离散时域傅立叶变换（Discrete Time Fourier Transform） 4. 周期性离散信号离散傅立叶变换（Discrete Fourier Transform） 其中，对于离散信号，我们主要关心离散傅立叶变换（DFT），因为计算机只能处理离散的数值信号，我们的最终目的是运用计算机来处理信号的。 傅立叶变换的重要性： 傅立叶变换是一种非常重要的信号处理技术，它可以将信号从时域转换到频域，以便更好地分析和处理信号。在信号处理领域中，傅立叶变换广泛应用于信号滤波、信号压缩、信号识别等方面。 傅立叶变换的优点： 傅立叶变换有很多优点，它可以将信号从时域转换到频域，以便更好地分析和处理信号。此外，傅立叶变换也可以将信号分解成不同的频率分量，以便更好地理解信号的性质。 傅立叶变换的实例： 下面是一个实数离散傅立叶变换（Real DFT）的例子： 我们有一个原始信号图像，信号的长度是16。然后，我们可以使用傅立叶变换将信号从时域转换到频域。我们可以得到信号的频谱图像。 傅立叶变换是一种非常重要的信号处理技术，它广泛应用于信号处理领域中。通过理解傅立叶变换，我们可以更好地分析和处理信号，从而提高信号处理的效率和效果。