Python For Data Science Cheat Sheet
NumPy Basics
Learn Python for Data Science Interactively at www.DataCamp.com
NumPy
DataCamp
Learn Python for Data Science Interactively
The NumPy library is the core library for scientific computing in
Python. It provides a high-performance multidimensional array
object, and tools for working with these arrays.
>>> import numpy as np
Use the following import convention:
Creating Arrays
>>> np.zeros((3,4)) Create an array of zeros
>>> np.ones((2,3,4),dtype=np.int16) Create an array of ones
>>> d = np.arange(10,25,5) Create an array of evenly
spaced values (step value)
>>> np.linspace(0,2,9) Create an array of evenly
spaced values (number of samples)
>>> e = np.full((2,2),7) Create a constant array
>>> f = np.eye(2) Create a 2X2 identity matrix
>>> np.random.random((2,2)) Create an array with random values
>>> np.empty((3,2)) Create an empty array
Array Mathematics
>>> g = a - b Subtraction
array([[-0.5, 0. , 0. ],
[-3. , -3. , -3. ]])
>>> np.subtract(a,b) Subtraction
>>> b + a Addition
array([[ 2.5, 4. , 6. ],
[ 5. , 7. , 9. ]])
>>> np.add(b,a) Addition
>>> a / b Division
array([[ 0.66666667, 1. , 1. ],
[ 0.25 , 0.4 , 0.5 ]])
>>> np.divide(a,b) Division
>>> a * b Multiplication
array([[ 1.5, 4. , 9. ],
[ 4. , 10. , 18. ]])
>>> np.multiply(a,b) Multiplication
>>> np.exp(b) Exponentiation
>>> np.sqrt(b) Square root
>>> np.sin(a) Print sines of an array
>>> np.cos(b) Element-wise cosine
>>> np.log(a) Element-wise natural logarithm
>>> e.dot(f) Dot product
array([[ 7., 7.],
[ 7., 7.]])
Subseing, Slicing, Indexing
>>> a.sum() Array-wise sum
>>> a.min() Array-wise minimum value
>>> b.max(axis=0) Maximum value of an array row
>>> b.cumsum(axis=1) Cumulative sum of the elements
>>> a.mean() Mean
>>> b.median() Median
>>> a.corrcoef() Correlation coefficient
>>> np.std(b) Standard deviation
Comparison
>>> a == b Element-wise comparison
array([[False, True, True],
[False, False, False]], dtype=bool)
>>> a < 2 Element-wise comparison
array([True, False, False], dtype=bool)
>>> np.array_equal(a, b) Array-wise comparison
1 2 3
1D array 2D array 3D array
1.5 2 3
4 5 6
Array Manipulation
NumPy Arrays
axis 0
axis 1
axis 0
axis 1
axis 2
Arithmetic Operations
Transposing Array
>>> i = np.transpose(b) Permute array dimensions
>>> i.T Permute array dimensions
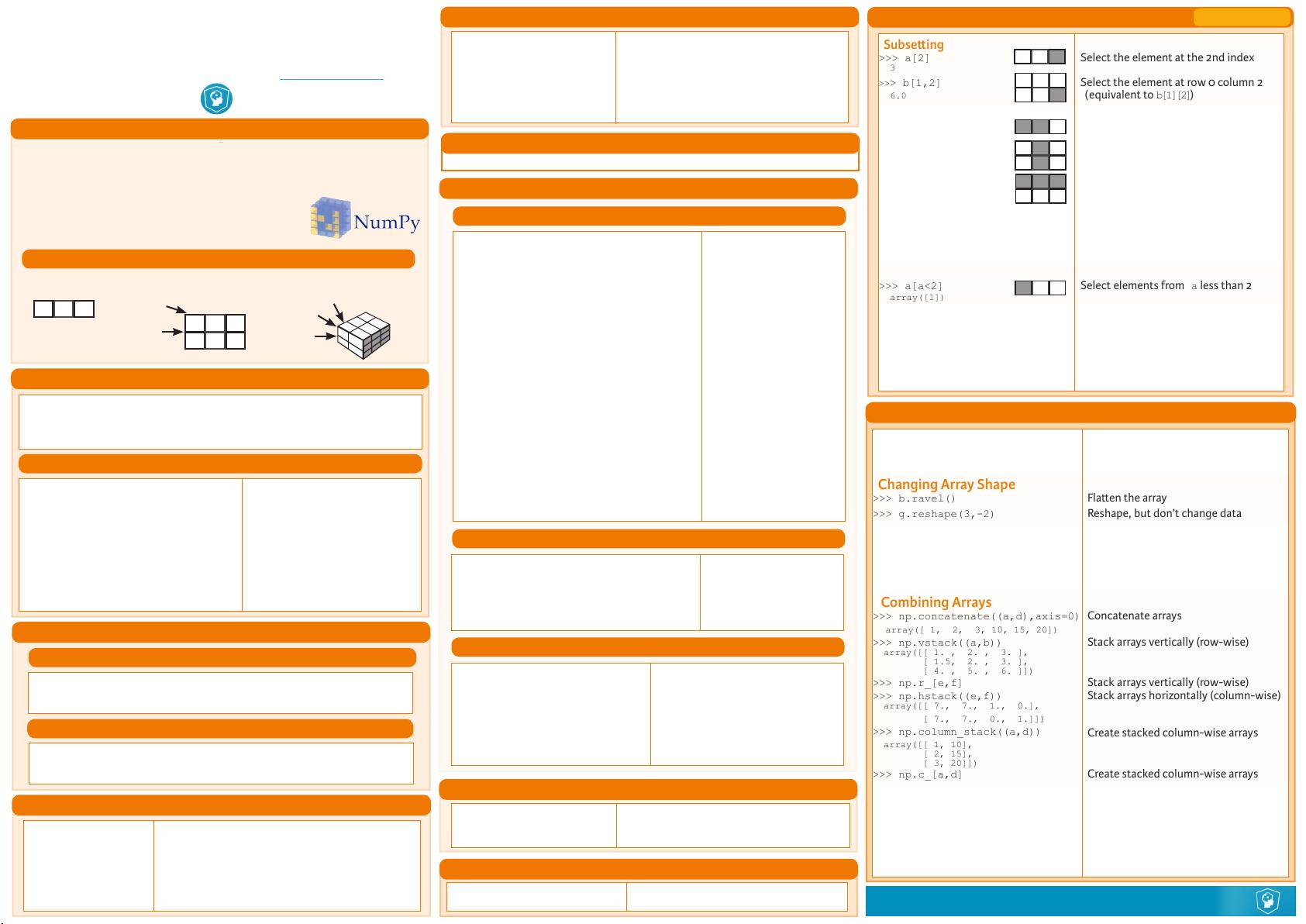
Changing Array Shape
>>> b.ravel() Flaen the array
>>> g.reshape(3,-2) Reshape, but don’t change data
Adding/Removing Elements
>>> h.resize((2,6)) Return a new array with shape (2,6)
>>> np.append(h,g) Append items to an array
>>> np.insert(a, 1, 5) Insert items in an array
>>> np.delete(a,[1]) Delete items from an array
Combining Arrays
>>> np.concatenate((a,d),axis=0) Concatenate arrays
array([ 1, 2, 3, 10, 15, 20])
>>> np.vstack((a,b)) Stack arrays vertically (row-wise)
array([[ 1. , 2. , 3. ],
[ 1.5, 2. , 3. ],
[ 4. , 5. , 6. ]])
>>> np.r_[e,f] Stack arrays vertically (row-wise)
>>> np.hstack((e,f)) Stack arrays horizontally (column-wise)
array([[ 7., 7., 1., 0.],
[ 7., 7., 0., 1.]])
>>> np.column_stack((a,d))
Create stacked column-wise arrays
array([[ 1, 10],
[ 2, 15],
[ 3, 20]])
>>> np.c_[a,d] Create stacked column-wise arrays
Spliing Arrays
>>> np.hsplit(a,3) Split the array horizontally at the 3rd
[array([1]),array([2]),array([3])] index
>>> np.vsplit(c,2) Split the array vertically at the 2nd index
[array([[[ 1.5, 2. , 1. ],
[ 4. , 5. , 6. ]]]),
array([[[ 3., 2., 3.],
[ 4., 5., 6.]]])]
Also see Lists
Subseing
>>> a[2] Select the element at the 2nd index
3
>>> b[1,2] Select the element at row 0 column 2
6.0 (equivalent to b[1][2])
Slicing
>>> a[0:2] Select items at index 0 and 1
array([1, 2])
>>> b[0:2,1] Select items at rows 0 and 1 in column 1
array([ 2., 5.])
>>> b[:1] Select all items at row 0
ar ra y( [[1.5, 2., 3.]]) (equivalent to b[0:1, :])
>>> c[1,...] Same as [1,:,:]
ar ra y( [[[ 3., 2., 1.],
[ 4., 5., 6.]]])
>>> a[ : :-1] Reversed array a
array([3, 2, 1])
Boolean Indexing
>>> a[a<2] Select elements from a less than 2
array([1])
Fancy Indexing
>>> b [[1, 0, 1, 0], [0, 1, 2, 0]] Select elements (1,0),(0,1),(1,2) and (0,0)
ar ra y( [ 4. , 2. , 6. , 1.5])
>>> b [[1, 0, 1, 0]][:,[0,1,2,0]] Select a subset of the matrix’s rows
ar ra y( [[ 4. ,5. , 6. , 4. ], and columns
[ 1.5, 2. , 3. , 1.5],
[ 4. , 5. , 6. , 4. ],
[ 1.5, 2. , 3. , 1.5]])
>>> a = np.array([1,2,3])
>>> b = np.array([(1.5,2,3), (4,5,6)], dtype = oat)
>>> c = np.array([[(1.5,2,3), (4,5,6)], [(3,2,1), (4,5,6)]],
dtype = oat)
Initial Placeholders
Aggregate Functions
>>> np.loadtxt("myle.txt")
>>> np.genfromtxt("my_le.csv", delimiter=',')
>>> np.savetxt("myarray.txt", a, delimiter=" ")
I/O
1 2 3
1.5 2
3
4 5 6
Copying Arrays
>>> h = a.view() Create a view of the array with the same data
>>> np.copy(a) Create a copy of the array
>>> h = a.copy() Create a deep copy of the array
Saving & Loading Text Files
Saving & Loading On Disk
>>> np.save('my_array', a)
>>> np.savez('array.npz', a, b)
>>> np.load('my_array.npy')
>>> a.shape Array dimensions
>>> len(a) Length of array
>>> b.ndim Number of array dimensions
>>> e.size Number of array elements
>>> b.dtype Data type of array elements
>>> b.dtype.name Name of data type
>>> b.astype(int) Convert an array to a different type
Inspecting Your Array
>>> np.info(np.ndarray.dtype)
Asking For Help
Sorting Arrays
>>> a.sort() Sort an array
>>> c.sort(axis=0) Sort the elements of an array's axis
Data Types
>>> np.int64 Signed 64-bit integer types
>>> np.oat32 Standard double-precision floating point
>>> np.complex Complex numbers represented by 128 floats
>>> np.bool Boolean type storing TRUE and FALSE values
>>> np.object Python object type
>>> np.string_ Fixed-length string type
>>> np.unicode_ Fixed-length unicode type
1 2 3
1.5 2 3
4 5 6
1.5 2 3
4 5 6
1 2 3
