根据给定的文件信息,我们可以将此PPT资料的核心知识点归纳为以下几个方面:
### 一、机械手运动的表示方法
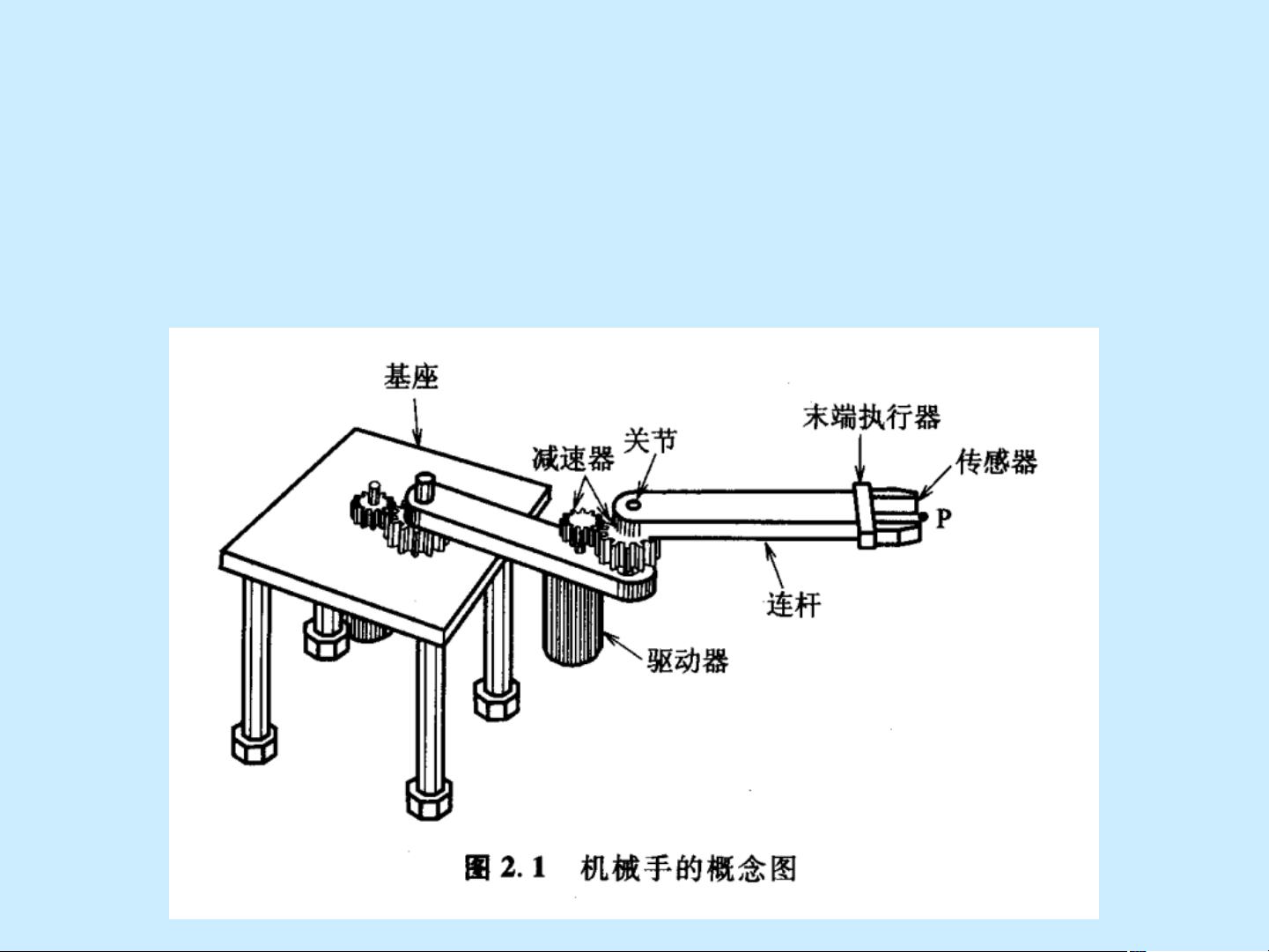
#### 2.1.1 机械手的结构
- **机械手概述**:机械手是一种能够模拟人类手臂功能进行各种操作的自动化设备。
- **结构分类**:
- **回转关节**:可以实现旋转运动,通常用于改变机械臂的方向。
- **棱柱关节**:实现直线运动,通常用于调整机械臂的伸缩。
- **关节变量**:用来描述各个关节位置的参数,是控制机械手动作的关键。
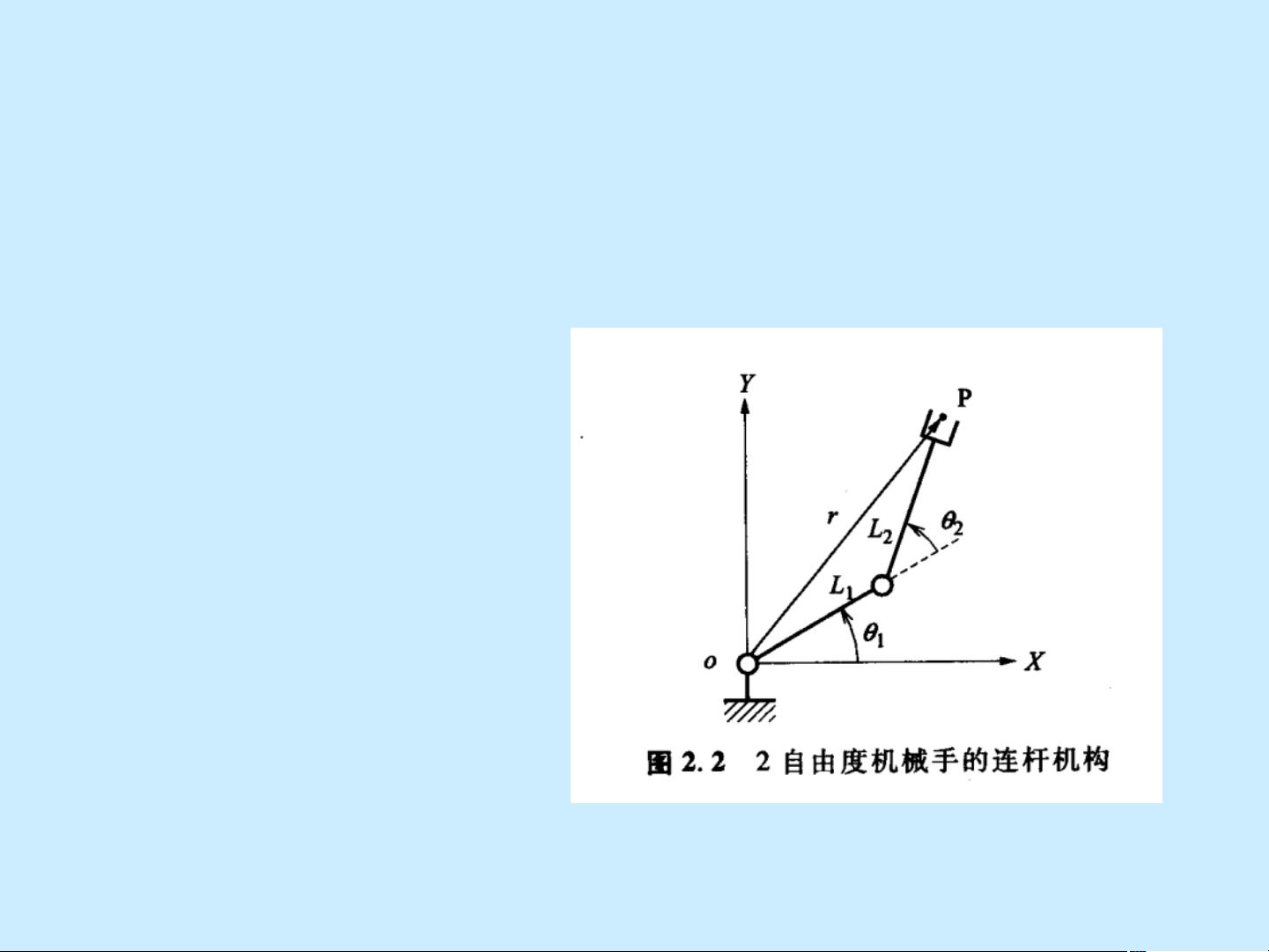
#### 2.1.2 机械手的机构和运动学
- **手爪位置**:通过一系列关节变量来确定机械手末端执行器的位置。
- **运动学方程式**:描述了关节变量与手爪位置之间的数学关系,即正向运动学问题。其基本形式可以表示为 \(\mathbf{r} = f(\boldsymbol{\theta})\),其中 \(\mathbf{r}\) 表示手爪位置,\(\boldsymbol{\theta}\) 表示关节变量。
- **正运动学与逆运动学**:
- **正运动学**:已知关节变量,求解手爪位置。
- **逆运动学**:已知手爪目标位置,求解相应的关节变量。
### 二、手爪位置和关节变量的关系
#### 2.2.1 手爪位置和姿态的表示方法
- **坐标系**:
- **基坐标系** (\(\Sigma_B\)):固定不动的参考坐标系。
- **手爪坐标系** (\(\Sigma_E\)):随着机械手末端执行器移动而变化的坐标系。
- **位置与姿态表示**:
- **位置向量** (\(Bp_E \in \mathbb{R}^{3 \times 1}\)):手爪坐标系原点相对于基坐标系的位置。
- **姿态变换矩阵** (\(BR_E \in \mathbb{R}^{3 \times 3}\)):描述手爪坐标系相对于基坐标系的姿态。
#### 2.2.2 姿态变换矩阵
- **坐标转换**:如果已知某点 \(P\) 在两个不同坐标系中的坐标分别为 \(\mathbf{p}_B\) 和 \(\mathbf{p}_E\),则可以通过姿态变换矩阵 \(BRA\) 来表示它们之间的关系,即 \(\mathbf{p}_B = BRA \cdot \mathbf{p}_E\)。
- **性质**:姿态变换矩阵具有特殊的性质,如行列式等于1等。
#### 2.2.3 齐次变换
- **定义**:齐次变换矩阵是一种4×4矩阵,可以同时描述位置和姿态的变化,常用于描述两个坐标系之间的相对位置和姿态关系。
- **应用**:
- **建模**:首先建立各个连杆的坐标系,并用连杆长度和关节变量计算相邻坐标系之间的位姿关系。
- **求解**:求得相邻坐标系之间的齐次变换矩阵后,可以进一步求解出整个机械手系统的总变换矩阵,从而得到末端执行器相对于基坐标系的位置和姿态。
### 三、雅可比矩阵
#### 2.3.1 雅可比矩阵的定义
- **概念**:雅可比矩阵是描述机械手末端执行器速度与关节速度之间关系的矩阵。
- **定义**:设正向运动学方程为 \(\mathbf{r} = f(\boldsymbol{\theta})\),则雅可比矩阵 \(J\) 可以定义为 \(\dot{\mathbf{r}} = J(\boldsymbol{\theta}) \cdot \dot{\boldsymbol{\theta}}\),其中 \(\dot{\mathbf{r}}\) 表示末端执行器的速度,\(\dot{\boldsymbol{\theta}}\) 表示关节速度。
- **冗余机器人**:当关节数量 \(n\) 大于末端执行器自由度 \(m\) 时(即 \(n > m\)),这样的机器人被称为冗余机器人,此时雅可比矩阵通常不是满秩的。
以上就是从给定文件中提取出来的关键知识点,涵盖了机械手运动的基础理论和关键技术,对于理解机械手的工作原理及其运动控制具有重要的意义。