第七章 遗传算法应用举例.pdf

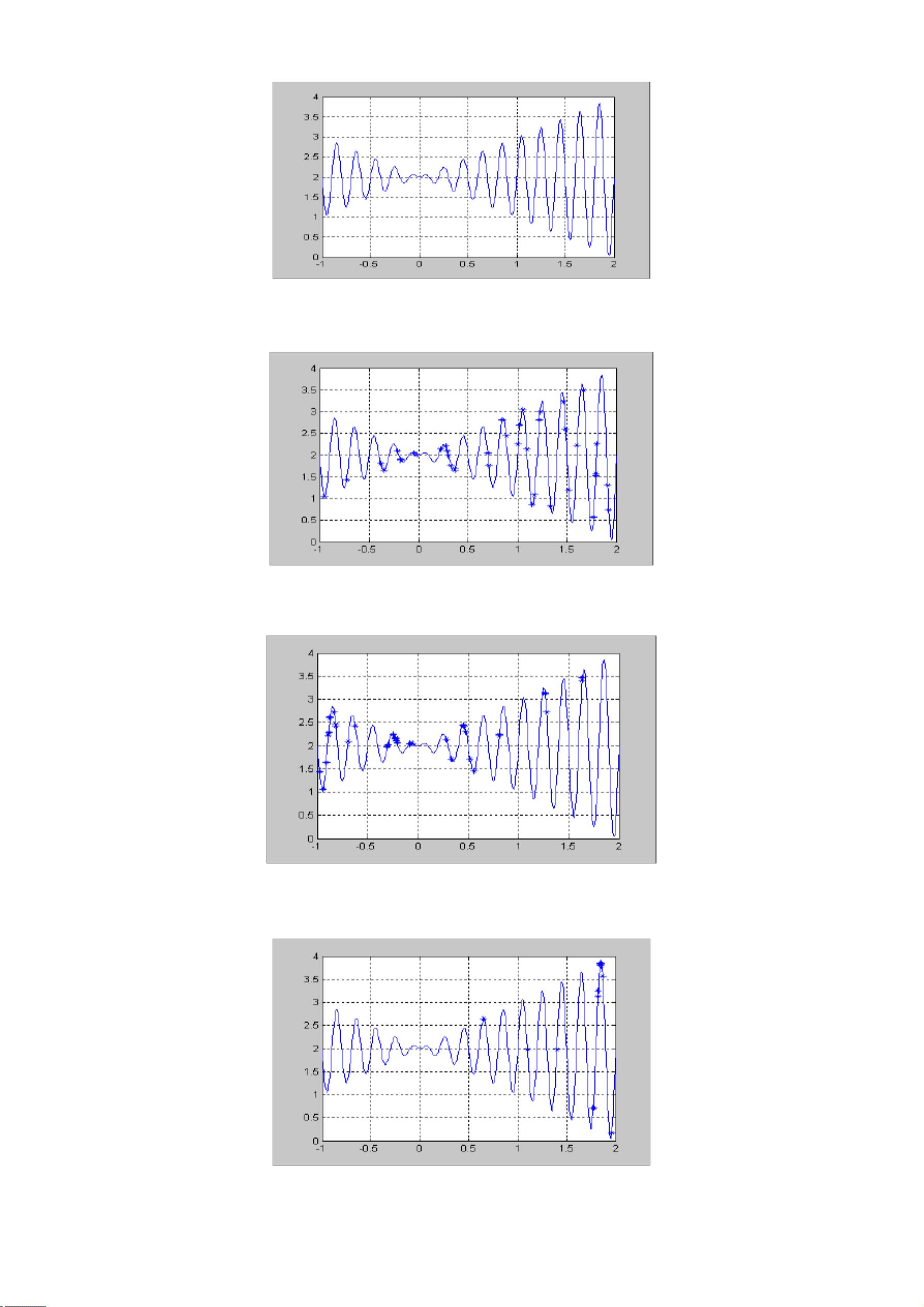
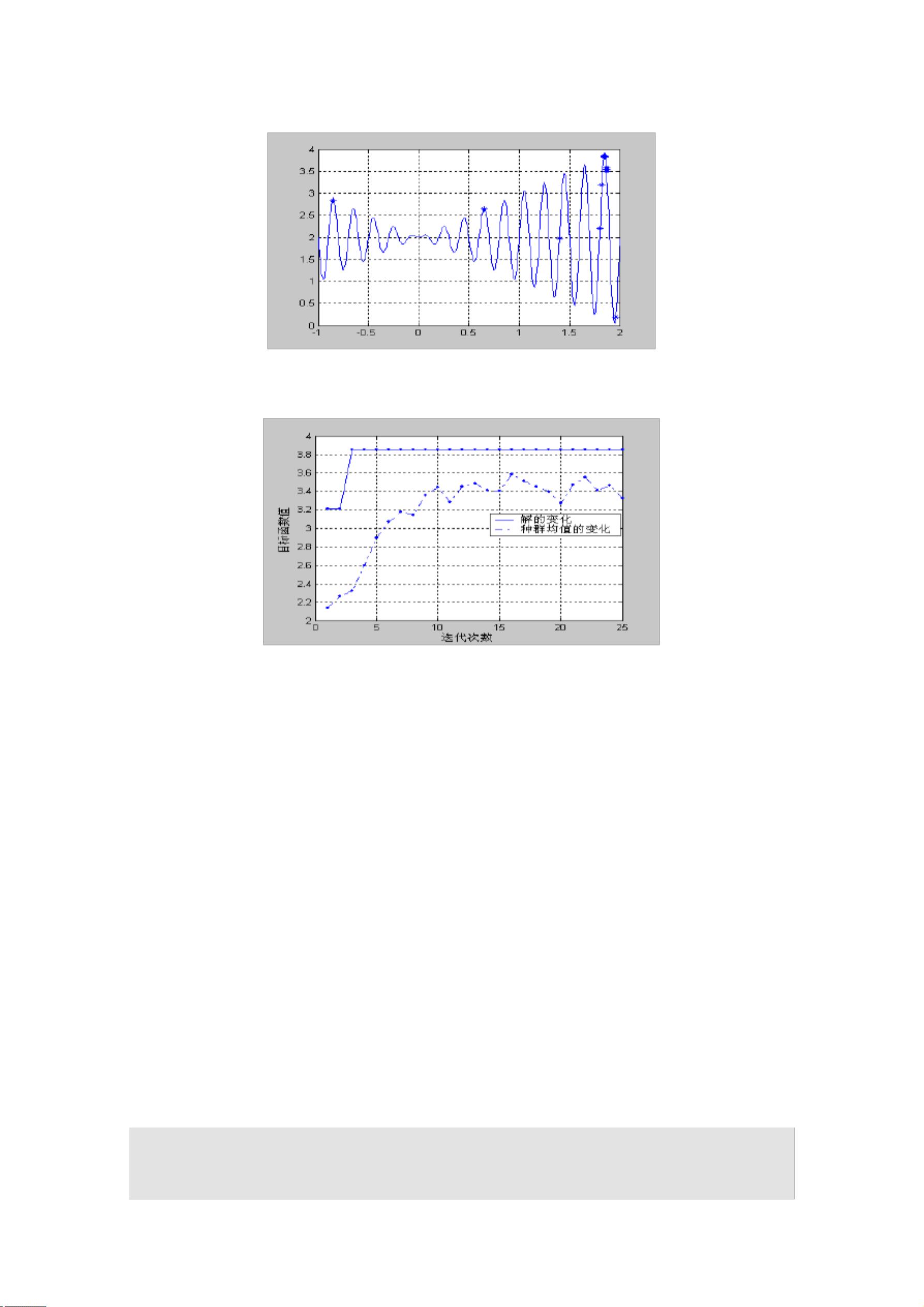
《第七章 遗传算法应用举例》章节深入探讨了如何运用遗传算法解决实际的优化问题，特别是针对一元函数优化。遗传算法是一种强大的搜索工具，适用于非线性、多模态、多目标等问题，无需了解问题的具体背景。随着遗传算法技术的发展，其在众多领域如函数优化、组合优化、自动控制、机器人学、图像处理等都有广泛应用。 在这个例子中，我们关注的是寻找一元函数 \( f(x) = x \cdot \sin(10\pi \cdot x) + 2.0 \) 在 \( x \in [-1,2] \) 范围内的最大值。遗传算法的实现采用了二进制编码，种群大小设为40，每个个体的长度为20，代沟（GenerationStrategy）设定为0.9，最大遗传代数为25。 MATLAB程序首先绘制函数曲线以直观展示问题。接着，定义了遗传算法的关键参数，包括个体数目、最大代数、精度、代沟以及区域描述器。`crtbp`函数用于创建初始种群，而`bs2rv`函数则将二进制编码转换为十进制。通过循环迭代，遗传算法依次执行适应度分配、选择、重组和变异操作。 适应度分配使用`ranking`函数，该函数默认使用等差为2的线性评估，对最适应的个体赋予最高适应度值。选择过程采用选择策略`sus`（随机遍历抽样），保留最适应的个体进入下一代。重组使用交叉操作`xovsp`，并结合变异操作`mut`来引入新的变化。`reins`函数负责回插入新种群，确保最适应的个体得以延续。 程序通过跟踪最佳解和种群平均值的变化来评估算法性能。在每一代结束后，程序会更新最优解，并在目标函数图上标记出来。同时，种群的平均值也会随着迭代进行追踪，以便观察算法的收敛趋势。 这个例子清晰地展示了遗传算法的基本流程和关键步骤，包括编码、初始化、评价、选择、重组和变异。通过这种方式，遗传算法可以解决复杂的优化问题，如旅行商问题、背包问题等，即使对于非线性函数也能找到全局最优解或近似最优解。在实际应用中，遗传算法的参数调整和编码方式是影响其性能的重要因素，需要根据具体问题进行优化。