09/05/2021
Binary Tree Overview
https://web.archive.org/web/20180704064217/http://faculty.cs.niu.edu/~mcmahon/CS241/Notes/bintree.html
1/4
The Wayback Machine - https://web.archive.org/web/20180704064217/http://faculty.cs.niu.edu/~mcmaho…
Binary Tree Overview
Formal Definition of a Binary Tree
A binary tree consists of a finite set of nodes that is either empty, or consists of one specially designated
node called the root of the binary tree, and the elements of two disjoint binary trees called the left subtree and
right subtree of the root.
Note that the definition above is recursive: we have defined a binary tree in terms of binary trees. This is
appropriate since recursion is an innate characteristic of tree structures.
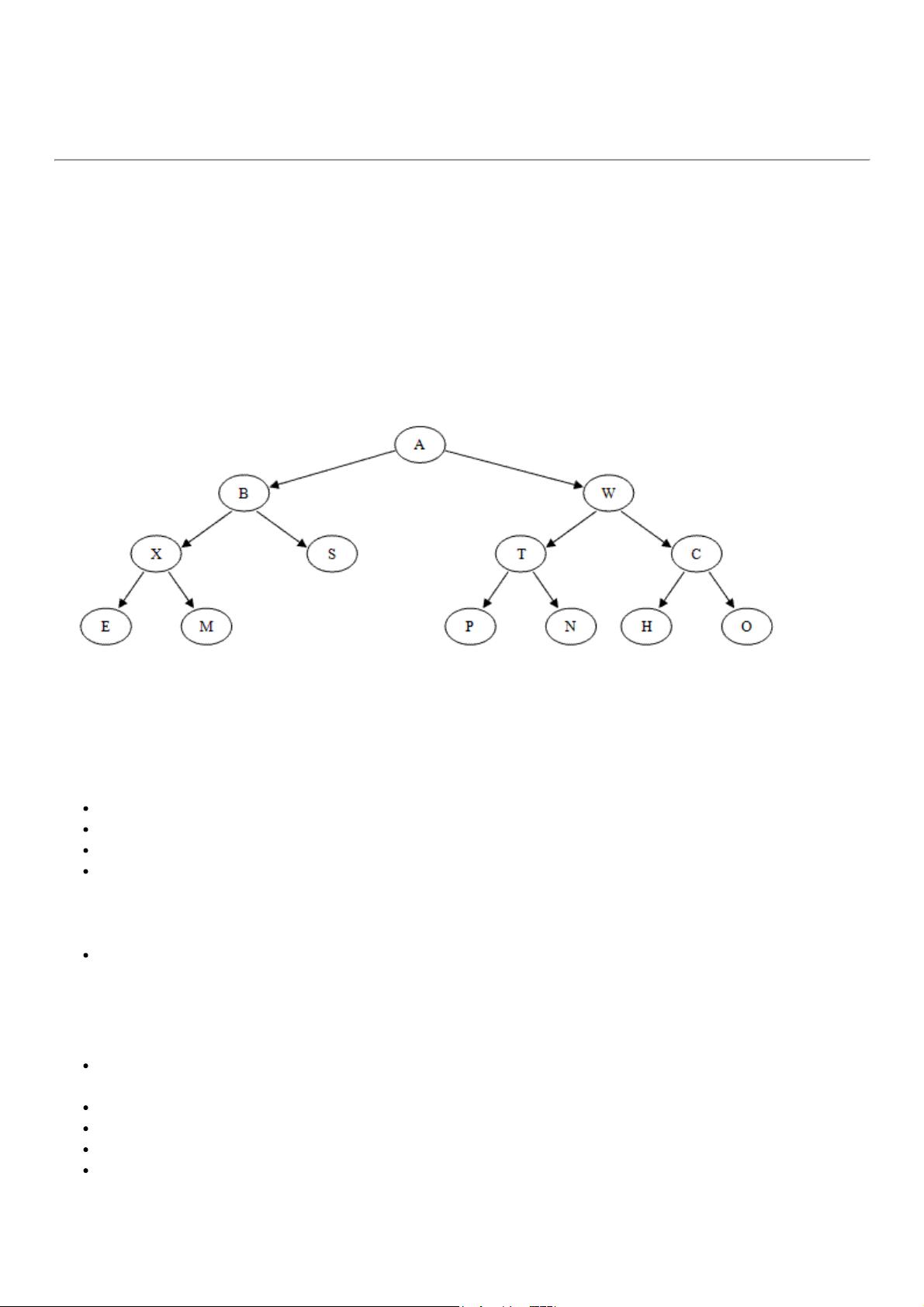
Diagram 1: A binary tree
Binary Tree Terminology
Tree terminology is generally derived from the terminology of family trees (specifically, the type of family
tree called a lineal chart).
Each root is said to be the parent of the roots of its subtrees.
Two nodes with the same parent are said to be siblings; they are the children of their parent.
The root node has no parent.
A great deal of tree processing takes advantage of the relationship between a parent and its children,
and we commonly say a directed edge (or simply an edge) extends from a parent to its children. Thus
edges connect a root with the roots of each subtree. An undirected edge extends in both directions
between a parent and a child.
Grandparent and grandchild relations can be defined in a similar manner; we could also extend this
terminology further if we wished (designating nodes as cousins, as an uncle or aunt, etc.).
Other Tree Terms
The number of subtrees of a node is called the degree of the node. In a binary tree, all nodes have
degree 0, 1, or 2.
A node of degree zero is called a terminal node or leaf node.
A non-leaf node is often called a branch node.
The degree of a tree is the maximum degree of a node in the tree. A binary tree is degree 2.
A directed path from node n
1
to n
k
is defined as a sequence of nodes n
1
, n
2
, ..., n
k
such that n
i
is the
parent of n
i
+1 for 1 <= i < k. An undirected path is a similar sequence of undirected edges. The length
of this path is the number of edges on the path, namely k – 1 (i.e., the number of nodes – 1). There is a
资源评论
