
抓住别人容易忽略的时间,圆自己的高考梦!
1
平度东方滨河中学
高一数学寒假自主学习园地

抓住别人容易忽略的时间,圆自己的高考梦!
2
前言
亲爱的同学们,青春的意义不仅是年轻,更是生命全力以赴的姿
态。青春因奋斗而美丽,人生因追求精彩。寒假是差距的开始。新一轮
的比拼由此拉开序幕,机会掌握在自己手中!
高一数学组全体老师衷心希望大家:
1、统筹安排,制定切实可行的假期学习计划。
科学的学习计划绝非一张时间表,它还包括内容表、落实方式及使
用表。最重要的一点是我们要提高执行力,坚持按照计划上写的做,这
是计划能够发挥作用的关键,否则就会沦为一纸空文。
2、复习的重点放在系统掌握所学知识,提高分析、解决问题的能
力上。
善于总结,善于思考是提高学习力的关键。因此,要求同学们对具
体知识点和能力点的有效总结,整理好笔记本;多动脑,多钻研,多分
析,完成此作业,以提高分析能力。
3、勿忘补弱。
在校学习期间补弱受到时间限制,而自由假期就为我们补弱提供了
极好的机会,希望同学们抓住良机,积极弥补自己的薄弱点,争取赶上
来。
4、学会感恩。
用一颗感恩的心看待一切,自然就会满眼阳光,心情舒畅。用一颗
感恩的心对亲人、老师、同学,自然会温暖人心,快乐自己。
谁拥有假期,谁拥有自主,谁就拥有未来。
抓住别人容易忽略的时间,圆自己的高考梦!
3
第一章
集合与常用逻辑用语
一、基础知识
(一)集合
1.元素与集合
(1)集合中元素的三个特性: 、 、
(2)元素与集合的关系是 ,表示符号分别为
(3)集合的表示方法:
2.集合间的基本关系
(1)子集: .
(2)真子集:若 A⊆B,且集合 B 中至少有一个元素不属于集合 A,则
(3)相等:若 A⊆B,且 B⊆A,则 .
(4)空集的性质:空集是 集合的子集,是任何 的真子集.
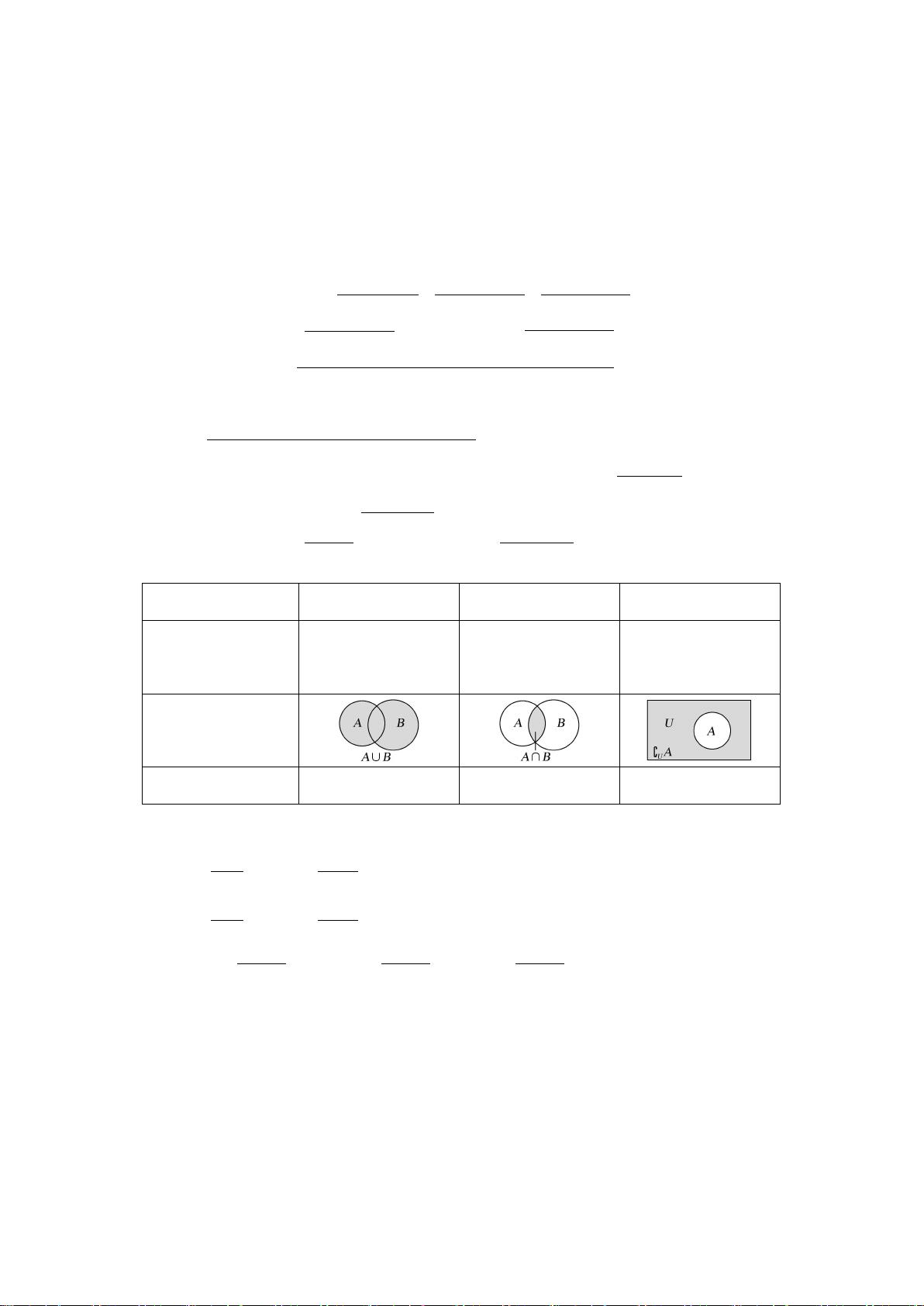
3.集合的基本运算
集合的并集
集合的交集
集合的补集
符号表示
A∪B
A∩B
若全集为 U,则集合
A 的补集为∁
U
A
图形表示
集合表示
4.集合的运算性质
(1)A∩A= ,A∩
= ,A∩B=B∩A.
(2)A∪A= ,A∪
= ,A∪B=B∪A.
(3)A∩(∁
U
A)= ,A∪(∁
U
A)= ,∁
U
(∁
U
A)= .
[提醒]
(1)若有限集 A 中有 n 个元素,则 A 的子集有 2
n
个,真子集有 2
n
-1 个.
(2)子集的传递性:A⊆B,B⊆C⇒A⊆C.
(3)A⊆B⇔A∩B=A⇔A∪B=B⇔∁
U
A⊇∁
U
B.
(4)∁
U
(A∩B)=(∁
U
A)∪(∁
U
B),∁
U
(A∪B)=(∁
U
A)∩(∁
U
B).
(二)常用逻辑用语

抓住别人容易忽略的时间,圆自己的高考梦!
4
1.充分条件、必要条件与充要条件的概念
若 p⇒q,则 p 是 q 的充分条件,q 是 p 的必要条件
p 是 q 的充分不必要条件
p 是 q 的必要不充分条件
p 是 q 的充要条件
p 是 q 的既不充分也不必要条件
2.全称量词与存在量词
(1)全称量词:短语“所有的”、“任意一个”等叫做全称量词,用符号“∀”表示.
(2)存在量词:短语“存在一个”、“至少有一个”等叫做存在量词,用符号“∃”表示.
3.全称命题和特称命题(命题 p 的否定记为
p
,读作“非 p”)
名称
形式
全称命题
特称命题
结构
对 M 中的任意一个 x,有 p(x)成立
存在 M 中的一个 x
0
,使 p(x
0
)成立
简记
否定
二、基本题型
(一) 集合的基本概念
例 1 (1)若集合 M={x||x|≤1},N={y|y=x
2
,|x|≤1},则 ( )
A.M=N B.M⊆N C.M∩N=
D.N⊆M
(2)若 x∈A,则
1
x
∈A,就称 A 是“伙伴关系”集合,集合 M=
32
2
1
01 ,,,,
的所有非空子
集中具有“伙伴关系”的集合的个数是( ) A.1 B.3 C.7 D.31
(二) 集合间的基本关系
例 2 已知集合 A={x|x
2
-5x-14≤0},集合 B={x|m+1<x<2m-1},若 B⊆A,则实数 m 的
取值范围为________.
变式:若将本例的集合 A 改为 A={x|x
2
-5x-14>0}.其它条件不变,则 m 的取值范围是
_______.
(三) 集合的运算

抓住别人容易忽略的时间,圆自己的高考梦!
5
例 3 设 U 为全集,A,B 是其两个子集,则“存在集合 C,使得 A⊆C,B⊆∁
U
C”是“A∩B
=
”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
(四)充分条件与必要条件的判断
例 4 设函数 f(x)=
2
mx
+
1
,x≥0,
-x-
1
x
,x<0.
则“m>1 是 f[f(-1)]>4”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
(五)充分条件、必要条件的应用
例 5 已知 P={x|x
2
-8x-20≤0},非空集合 S={x|1-m≤x≤1+m}.若 x∈P 是 x∈S 的必要
条件,求 m 的取值范围.
【迁移探究 1】条件不变,若 x∈P 是 x∈S 的必要不充分条件,求 m 的取值范围.
【迁移探究 2】条件不变,若 x∈P 的必要条件是 x∈S,求 m 的取值范围.
【迁移探究 3】条件不变,问是否存在实数 m,使 x∈P 是 x∈S 的充要条件?并说明理由.
(六)全称量词与存在量词
例 6 已知 f(x)=ln(x
2
+1),g(x)=
x
2
1
-m,若对∀x
1
∈[0,3],∃x
2
∈[1,2],使得 f(x
1
)≥g(x
2
),
则实数 m 的取值范围是________.
变式 若将“∃x
2
∈[1,2]”改为“∀x
2
∈[1,2]”,其他条件不变,则实数 m 的取值范围是
____________.
答案 例 1 (1)D (2)B 例 2 (-∞,4] (-∞,2]∪[6,+∞) 例 3 C 例 4 A
例 5 [0,3] [9,+∞) m 不存在 例 6
,,
2
1
4
1
三、复习检测
四、1.集合 A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则 M 中元素的个
数为( )



















