Tutorial3_DTSystems solutions.pdf

### 教程3：离散时间系统解决方案 #### 一、移动平均滤波器 **背景与应用场景** 在金融市场的股票分析中，每日收盘价由于波动频繁，很难准确反映股票的真实表现趋势。为了平滑这种短期波动并揭示更长期的趋势，可以采用移动平均滤波器。例如，使用过去五天（包括当前日期）的日收盘价计算每周的表现指标。 **问题与解答** 1. **写出差分方程** 给定输入信号 \(x[n]\) 为第 \(n\) 天的市场收盘值，\(y[n]\) 表示经过移动平均处理后的输出，则对于一个5日移动平均滤波器，其差分方程表示为： \[ y[n] = \frac{1}{5} (x[n] + x[n - 1] + x[n - 2] + x[n - 3] + x[n - 4]) \] 其中，\(x[n]\) 表示第 \(n\) 天的收盘值，而 \(x[n-k]\) 表示第 \(n-k\) 天的收盘值。 2. **实现5日移动平均滤波器** 使用时间延迟（单位延迟 \(D\)）和乘法器元素来实现该滤波器。具体来说，可以通过以下结构实现： - 输入 \(x[n]\) 经过一个单位延迟 \(D\) 后变为 \(x[n-1]\)。 - 输入 \(x[n]\) 和经过一次延迟的 \(x[n-1]\) 再次分别通过两个单位延迟后变为 \(x[n-2]\) 和 \(x[n-3]\)。 - 最终，通过四个单位延迟，可以获得 \(x[n-4]\)。 - 将这些延迟后的信号相加，并将结果乘以系数 \(\frac{1}{5}\)，即可得到最终的输出 \(y[n]\)。 图形表示如下： \[ y[n] = \frac{1}{5} (x[n] + D\{x[n]\} + D^2\{x[n]\} + D^3\{x[n]\} + D^4\{x[n]\}) \] 其中，\(D^k\) 表示经过 \(k\) 次单位延迟。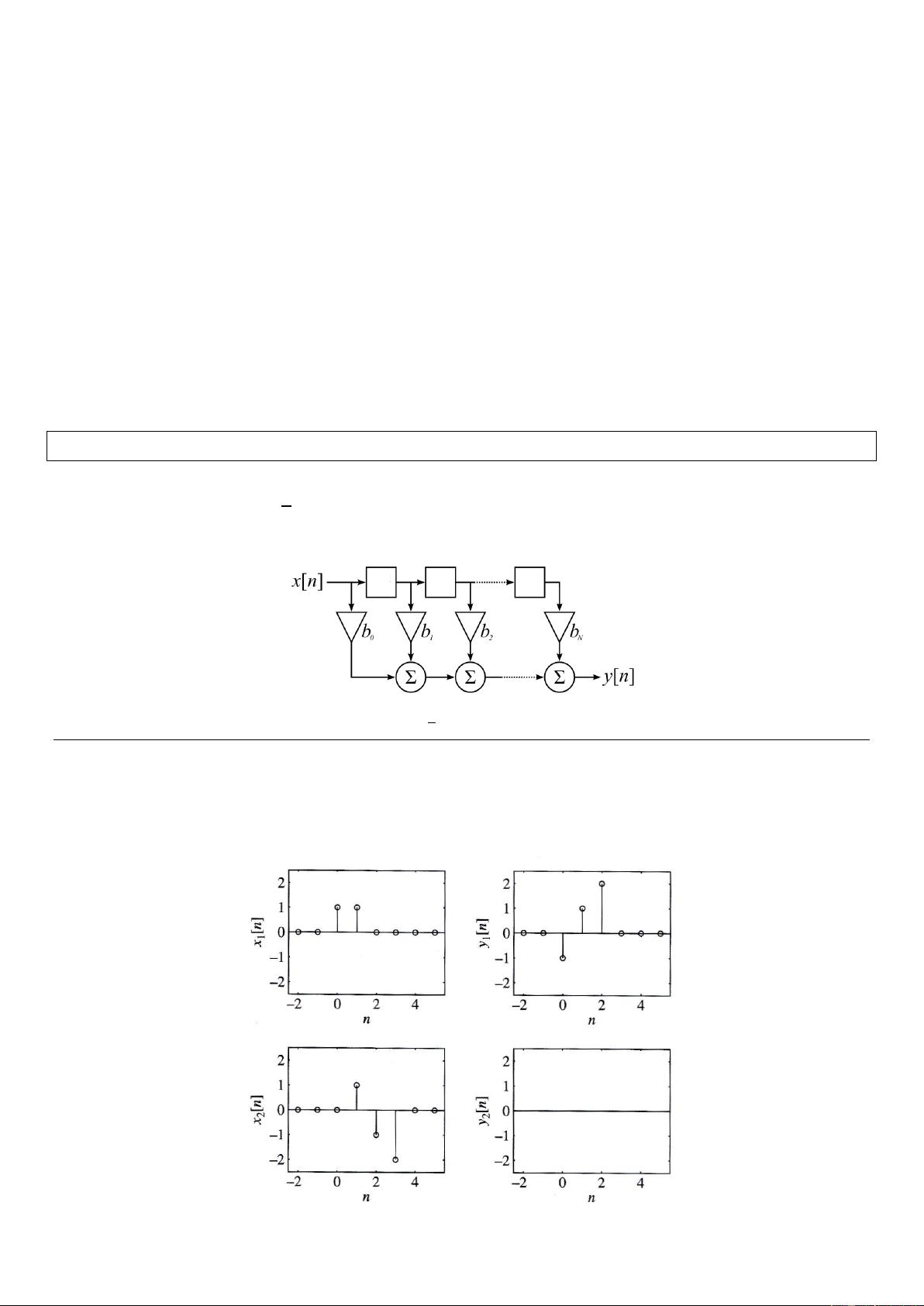 #### 二、线性时不变系统的输出响应 **问题与解答** 考虑一个线性时不变系统，当输入为 \(x_1[n]\) 时，输出为 \(y_1[n]\)。现在，如果输入变为 \(x_2[n]\)，需要确定并画出新的输出 \(y_2[n]\)。 1. **利用线性性质求解** 我们知道 \(y_1[n] = T\{x_1[n]\}\)。利用系统的线性性质，可以通过 \(x_2[n]\) 的表达式推导出 \(y_2[n]\)。 若将 \(x_2[n]\) 表达为 \(x_2[n] = \sum a_k x_1[n-k]\)，则有： \[ y_2[n] = \sum a_k T\{x_1[n-k]\} = \sum a_k y_1[n-k] \] 接下来的关键是找到使上式成立的最小参数集 \(\{a_k, k\}\)。 2. **参数确定** 通过观察发现： \[ x_2[n] = x_1[n-1] - 2x_1[n-2] \] 因此，可以得出： \[ y_2[n] = y_1[n-1] - 2y_1[n-2] \] 由此，可以绘制出 \(y_2[n]\) 的图形。 #### 三、LTI系统的总响应 **问题** 计算给定LTI系统由差分方程描述的总响应，其中： \[ y[n] + 2y[n-1] + y[n-2] = 2x[n] - x[n-1] \] 输入信号 \(x[n] = (3)^{-n}u[n]\)，初始条件未知。 **解答** 本部分题目给出了一个LTI系统的差分方程以及输入信号的形式，但没有给出具体的初始条件。因此，我们暂时无法计算出完整的总响应。不过，可以简要介绍如何根据已知条件计算总响应的一般步骤： 1. **求解齐次方程** 需要求解对应的齐次方程，即： \[ y_h[n] + 2y_h[n-1] + y_h[n-2] = 0 \] 这一步是为了获得系统的齐次解 \(y_h[n]\)。 2. **求解特解** 接着，需要根据输入信号 \(x[n]\) 形式求解系统的特解 \(y_p[n]\)。在这个例子中，\(x[n] = (3)^{-n}u[n]\)，因此需要寻找与输入信号形式相符的特解。 3. **合并求得总响应** 将齐次解 \(y_h[n]\) 与特解 \(y_p[n]\) 相加，并根据初始条件求解待定系数，从而获得系统的总响应 \(y[n]\)。 由于题目中没有给出具体的初始条件，无法进一步计算出确切的结果。但上述步骤为我们提供了一个解决问题的基本框架。