L6562中文.pdf

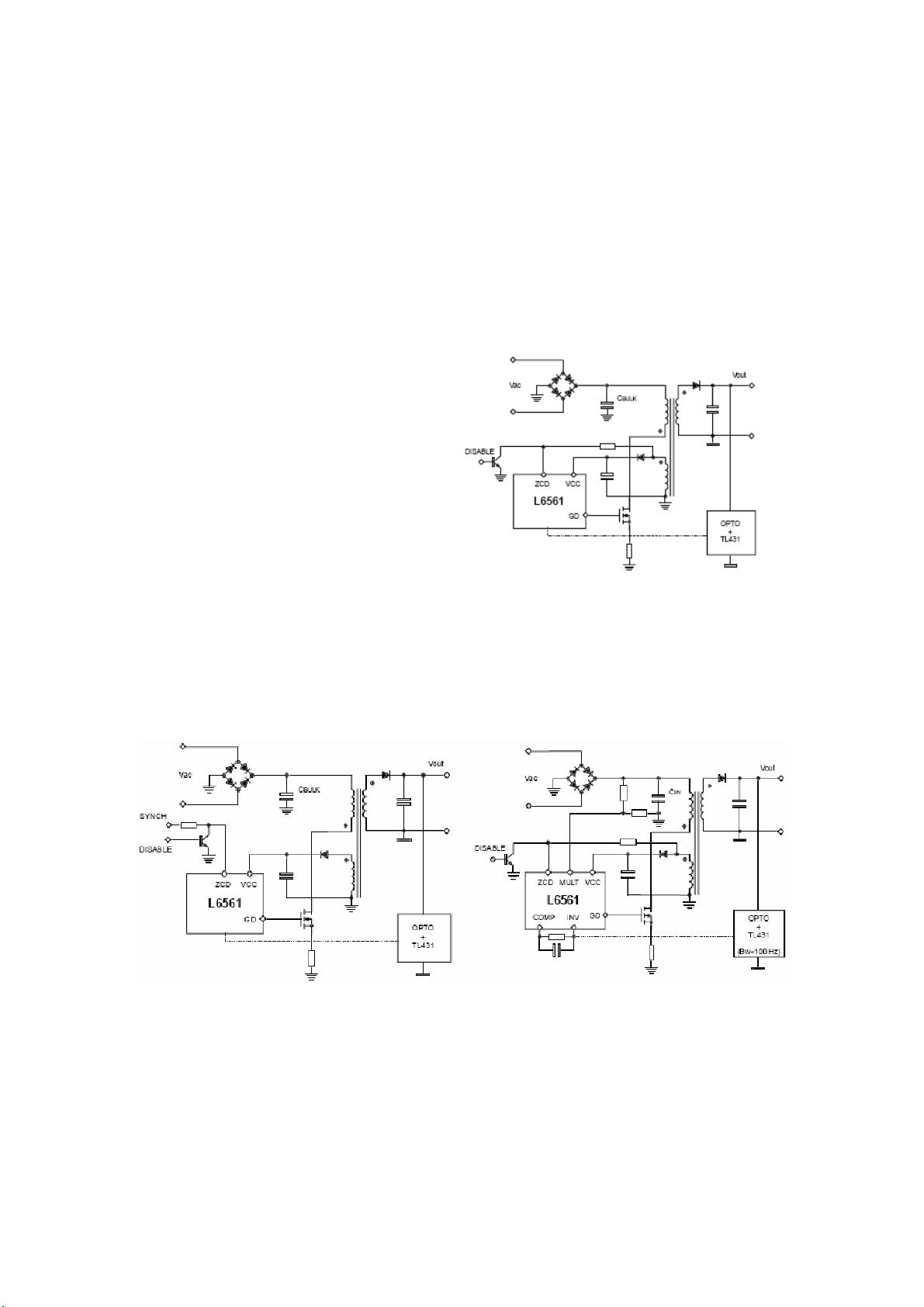
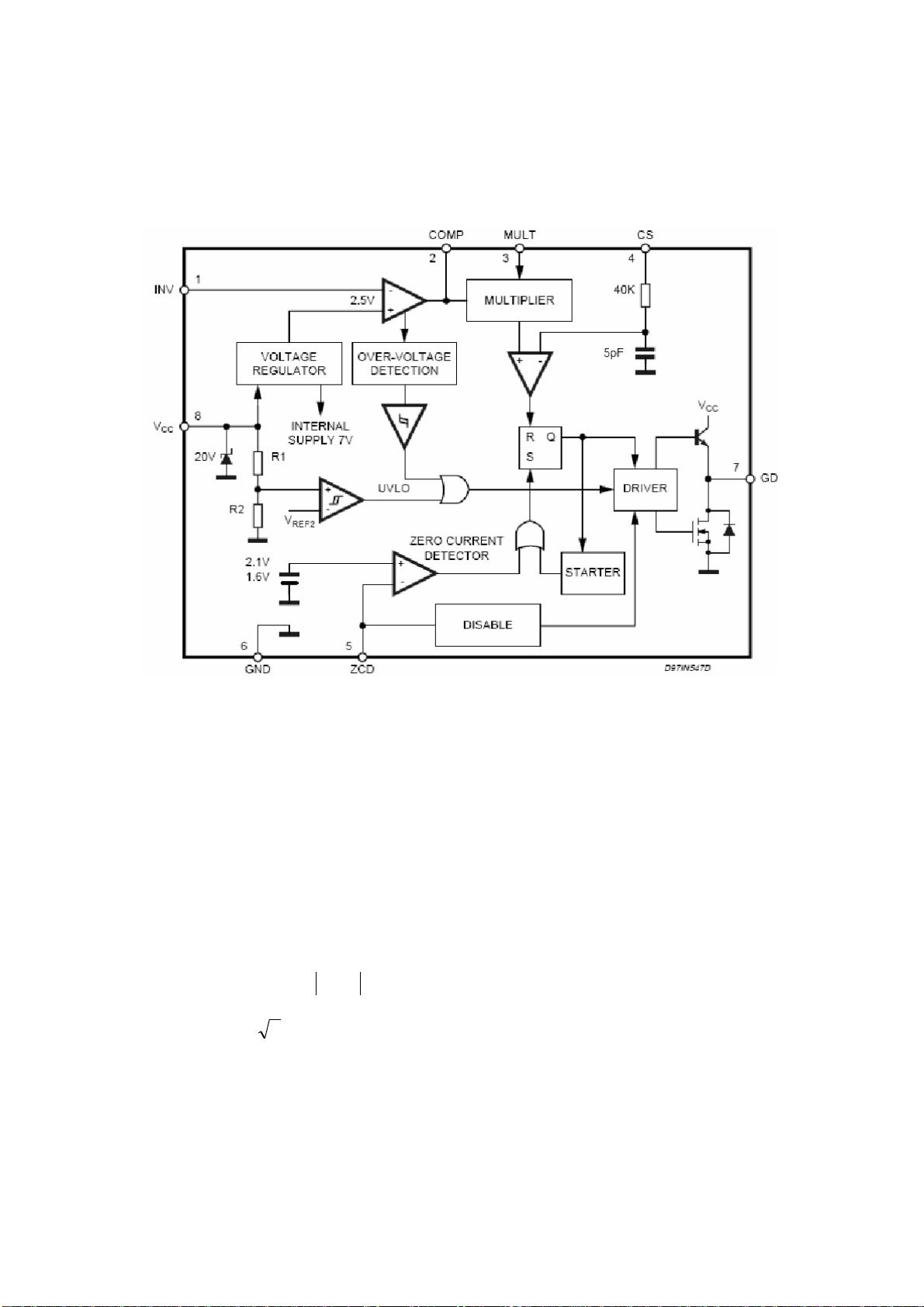
### L6561高功率因数反激变换器设计详解 #### 引言 L6561作为一款高性能的集成电路，专为设计高功率因数(Power Factor Correction, PFC)反激变换器而优化。反激变换器是一种常见的非隔离型DC-DC转换器，广泛应用于各种电子设备中，如适配器、充电器和低功率开关电源。L6561芯片通过其独特的控制策略，能够在保持高效的同时，显著提升功率因数，减少输入电流的谐波失真，从而满足严格的电磁兼容性(EMC)标准。 #### 设计原理 L6561支持三种不同的电路设计，分别是临界电流连续模式、固定频率模式以及高PF模式。其中，高PF模式是最常用的一种，它使变换器工作在临界连续模式下，利用极小的输入电容和接近正弦波的输入电压，以实现高功率因数。 ##### 临界连续模式 在临界连续模式下，L6561能够调整开关频率，使其刚好在电感电流连续和断续的边界上工作。这种模式下的变换器效率较高，尤其是在重载条件下，可以达到90%左右。MOSFET的导通损耗降低，整流桥的损耗也得以减少，从而降低了对散热器的需求。 ##### 固定频率模式 相比之下，固定频率模式下的变换器使用同步信号进行控制，与传统的PWM控制器类似，但在轻载情况下仍能保持较高的效率。这是因为L6561具有较低的静态电流消耗，可以有效减少启动电阻和自供电源的损耗。 #### 高PF反激变换器的优势 使用L6561设计的高PF反激变换器，相较于传统设计，具有多方面的优势： 1. **小尺寸输入电容**：在相同的功率等级下，输入电容的体积可以减小200倍，这意味着可以采用更小巧、更经济的薄膜电容替代大型且昂贵的电解电容。 2. **高效率**：在重载状态下，效率可达90%，这得益于临界连续模式下MOSFET的低导通损耗和高功率因数对整流桥损耗的减少。 3. **简化设计**：零部件数量的减少不仅降低了采购难度，还降低了装配成本。 4. **轻载高效**：即使在轻载条件下，L6561也能保持较高的效率，这归功于其低静态电流消耗，使得基于L6561的高PF反激变换器轻松满足诸如Blue Angel Relation等节能标准。 #### 内部机制与设计方程 L6561的内部架构设计使其能够精确控制反激变换器的工作状态。通过乘法器接收整流后的正弦波电压，L6561能够确保变换器在临界连续模式下工作。峰值初级电流与电网电压成正比，而次级电流则受初级电流和变压器匝比的影响。 #### 定时关系与工作模式 在临界连续模式下，L6561控制的功率开关导通时间是恒定的，与Boost变换器中的情况相似。然而，截止时间是可变的，受到输出电压和次级电流的影响。这种设计使得变换器能够动态调整开关周期，以维持电感电流的连续性和稳定性。 #### 结论 基于L6561的高PF反激变换器设计，通过优化电路结构和控制策略，实现了在保持高效率的同时提升功率因数的目标。这种设计特别适用于那些对效率和体积有严格要求的应用场景，如便携式电子设备的充电器和适配器。虽然存在一定的局限性，例如输出纹波和瞬态响应等问题，但整体而言，L6561提供的解决方案为电子设备制造商提供了更加灵活和高效的电源管理选项。