没有合适的资源?快使用搜索试试~ 我知道了~
数学建模-下料问题.pdf
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 78 浏览量
2022-05-02
16:57:50
上传
评论
收藏 296KB PDF 举报
温馨提示

试读
18页
数学建模-下料问题
资源推荐
资源详情
资源评论

生产中通过切割、剪裁、冲压等手段,将
原材料加工成所需大小
钢管和易拉罐下料
原料下料问题
按照工艺要求,确定下料方案,使所用材
料最省,或利润最大
问题1. 如何下料最节省 ?
例1 钢管下料
问题2. 客户增加需求:
原料钢管:每根19米
4米50根 6米20根
8米15根
客户需求
节省的标准是什么?
由于采用不同切割模式太多,会增加生产和管理成
本,规定切割模式不能超过3种。如何下料最节省?
5米10根
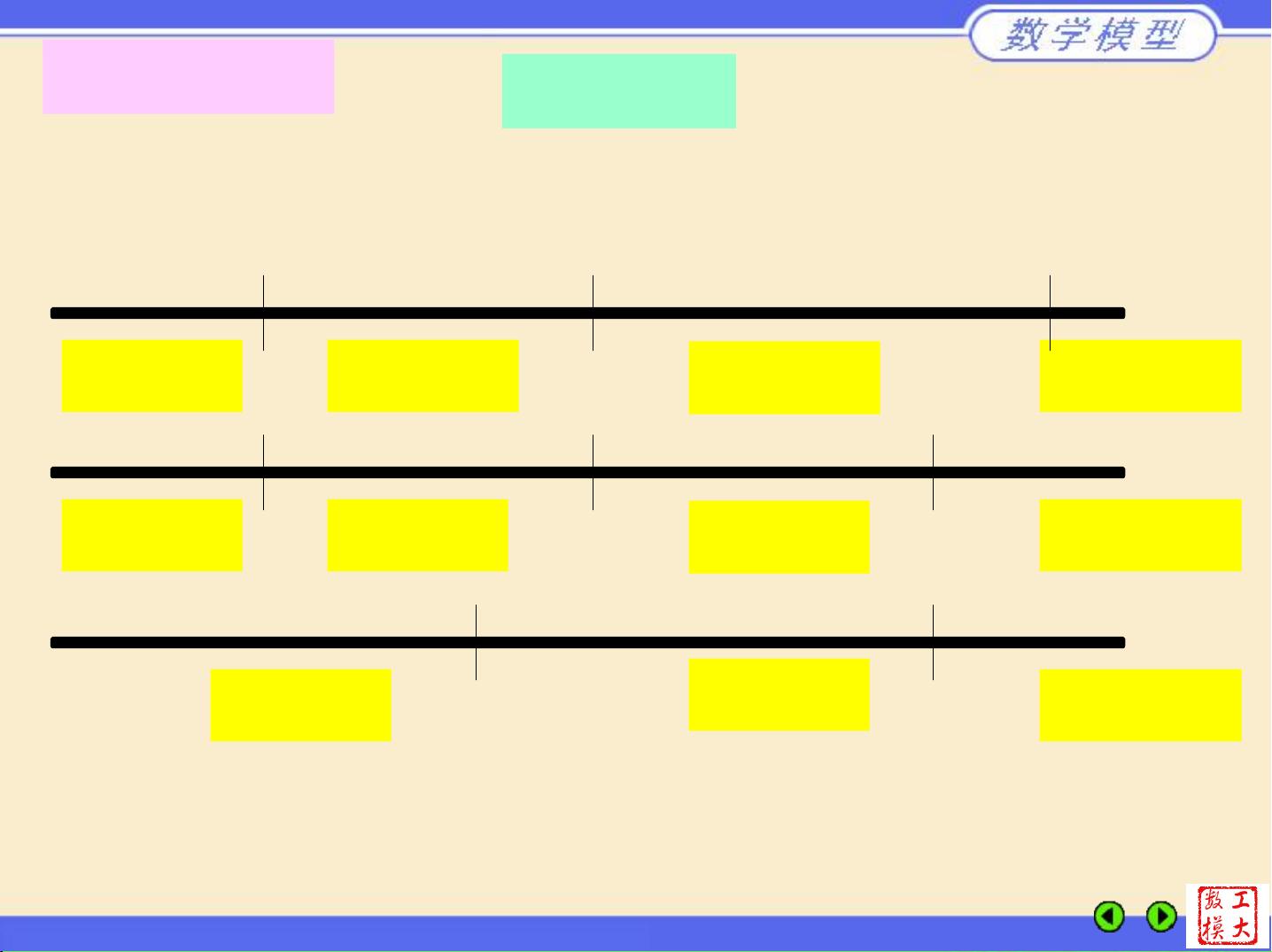
按照客户需要在一根原料钢管上安排切割的一种组合。
切割模式
余料1米
4米1根 6米1根
8米1根
余料3米4米1根 6米1根
6米1根
合理切割模式的余料应小于客户需要钢管的最小尺寸
余料3米8米1根
8米1根
钢管下料

为满足客户需要,按照哪些种合理模式,每种模式切
割多少根原料钢管,最为节省?
合理切割模式
2. 所用原料钢管总根数最少
模式
4米钢管根数 6米钢管根数 8米钢管根数 余料(米)
1
4 0 0 3
2
3 1 0 1
3
2 0 1 3
4
1 2 0 3
5
1 1 1 1
6
0 3 0 1
7
0 0 2 3
钢管下料问题1
两种
标准
1. 原料钢管剩余总余量最小
剩余17页未读,继续阅读
资源评论

普通网友
- 粉丝: 12w+
- 资源: 9337
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
