数学分布(泊松分布、二项分布、正态分布、均匀分布、指数分布)+生存分析+贝叶斯概率公式+全概率公式 (2).docx

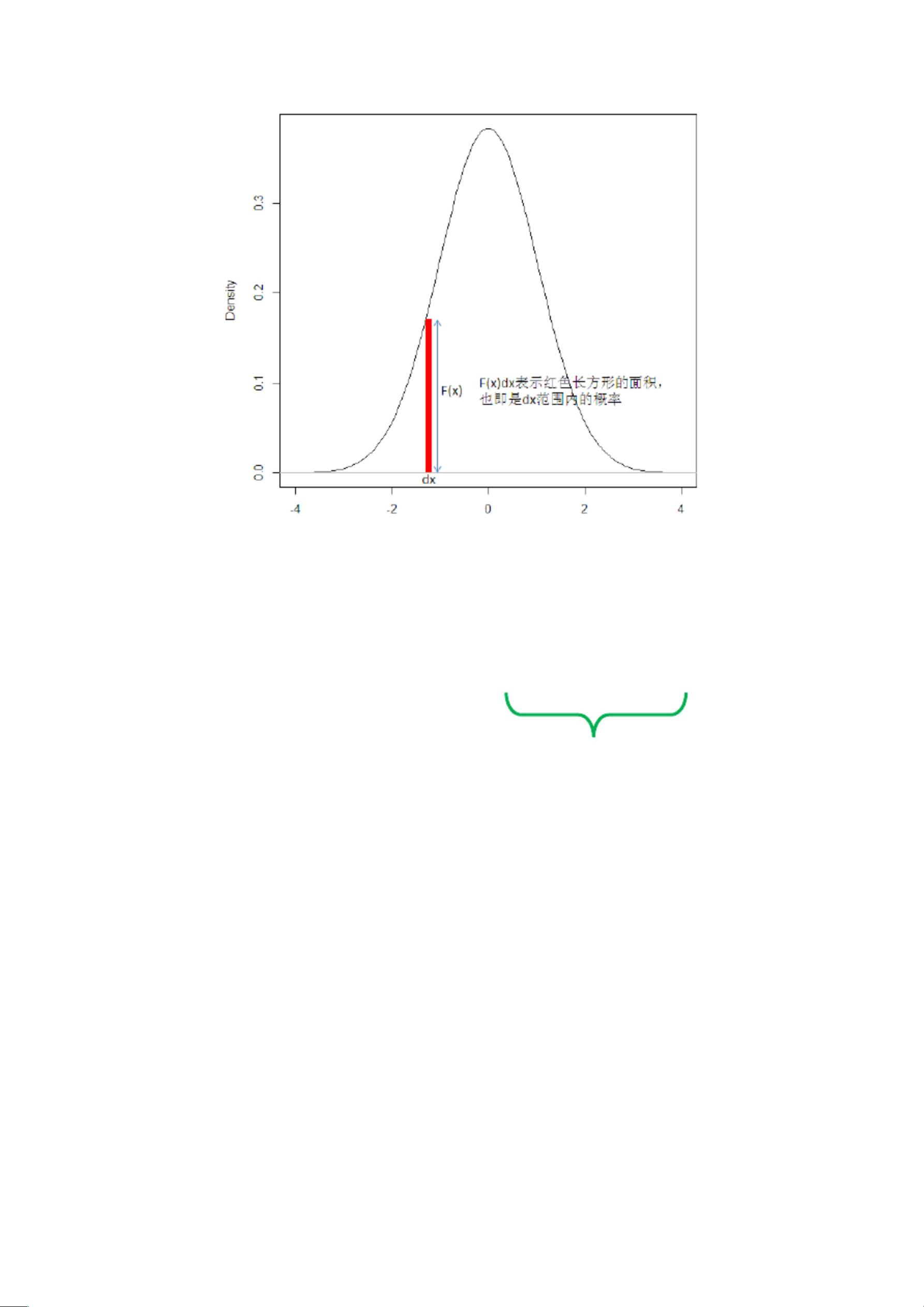
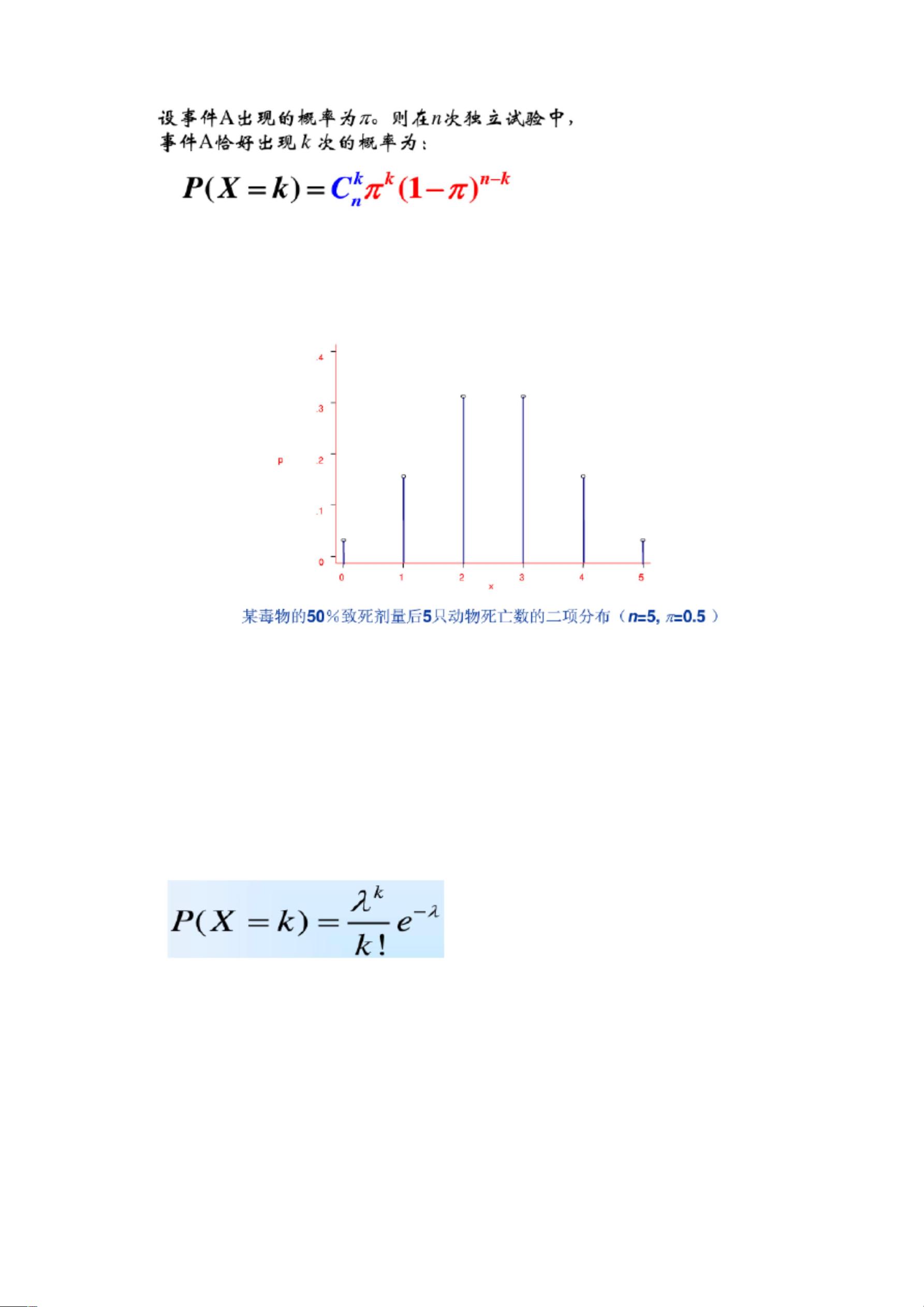
在统计学和概率论中，数学分布是用来描述随机变量可能出现的各种结果及其概率的模型。这里提到了几种重要的数学分布： 1. **泊松分布**（Poisson Distribution）：泊松分布通常用来描述在一定时间或空间区域内，独立事件发生次数的概率分布。如果一个事件的发生是独立且均匀的，那么在一段时间或空间内的事件计数就可能遵循泊松分布。例如，描述电话交换台在一小时内接到呼叫的次数。 2. **二项分布**（Binomial Distribution）：二项分布适用于只有两种可能结果的独立重复试验，如抛硬币。在一定次数的试验中，成功（如正面朝上）出现的次数遵循二项分布。其概率公式为P(X=k) = C(n, k) * p^k * (1-p)^(n-k)，其中C(n, k)是组合数，n是试验次数，p是单次试验成功的概率。 3. **正态分布**（Normal Distribution）或高斯分布：正态分布是一种连续分布，广泛用于描述许多自然现象的数据，如人的身高、体重等。其概率密度函数呈钟形曲线，均值μ决定了中心位置，标准差σ决定了分布的宽度。若样本量足够大，样本均值通常会接近正态分布。 4. **均匀分布**（Uniform Distribution）：均匀分布包括连续型和离散型，其中每个结果出现的概率相同。在连续型均匀分布中，概率密度函数在整个区间内是常数；在离散型均匀分布中，所有可能的结果概率相等。 5. **指数分布**（Exponential Distribution）：指数分布常用于描述等待时间直到某一事件首次发生的分布，如设备故障间隔时间。它是连续型的，每个时间点上发生事件的概率是常数。 6. **生存分析**（Survival Analysis）：生存分析关注的是研究对象的生存时间，如医学研究中患者的存活时间。它不仅考虑生存时间，还考虑失访和右截尾数据等问题，帮助分析不同因素对生存时间的影响。 7. **贝叶斯公式**（Bayes' Formula）：贝叶斯公式是概率论中的一个基本工具，用于更新先验概率（P(Bi)）以获得后验概率（P(Bi|A)），在已知证据A的情况下。公式为P(Bi|A) = P(A|Bi) * P(Bi) / P(A)，其中P(A|Bi)是似然性，P(Bi|A)是后验概率，P(Bi)是先验概率，而P(A)是证据A的证据因子。 8. **全概率公式**（Law of Total Probability）：全概率公式用于计算不知道事件B属于哪个子集的情况下，事件B发生的概率。如果事件B可以被不重叠的事件B1, B2, ..., Bn覆盖，且P(Bi)>0，那么P(B) = P(B|B1) * P(B1) + P(B|B2) * P(B2) + ... + P(B|Bn) * P(Bn)。 此外，还提到了抽样分布，如t分布和χ²分布，它们在假设检验和置信区间的构建中扮演重要角色。t分布用于小样本情况下估计总体均值，χ²分布则常用于检验正态性和独立性。F分布是t分布和χ²分布的比率，常见于方差分析（ANOVA）和方差齐性检验中。 通过理解和应用这些数学分布以及生存分析和贝叶斯公式，我们可以更好地理解和预测概率性问题，从而在统计推断、风险评估和决策制定中发挥作用。