没有合适的资源?快使用搜索试试~ 我知道了~
资源详情
资源评论
资源推荐

一、题目要求
1.用 SPSS 软件练习建立多元线性回归方程,分析数据的多重共线性,利用后退
法和逐步回归法选择变量,练习用岭回归方法处理该模型数据并作比较
2.用 SPSS 软件练习建立模型的非线性回归方程
二、数据分析
(一)题目:课本 7.6
1、数据
一家大型商业银行有多家分行,近年来,该银行的贷款额平稳增长,但不良贷款
额也有较大比例的提高为弄清楚不良贷款形成的原因,希望利用银行业务的有关数据
做些定量分析,以便找出控制不良贷款的方法。下表是该银行所属 25 甲分行 2002 年
的有关业务数据。
分行编号 不良贷款
y
各项贷款余
额
x1
本年累计应
收贷款
x2
贷款项目
个数
x3
本年固定资
产投资额
x4
1 0.9 67.3 6.8 5 51.9
2 1.1 111.3 19.8 16 90.9
3 4.8 173 7.7 17 73.7
4 3.2 80.8 7.2 10 14.5
5 7.8 199.7 16.5 19 63.2
6 2.7 16.2 2.2 1 2.2
7 1.6 107.4 10.7 17 20.2
8 12.5 185.4 27.1 18 43.8
9 1 96.1 1.7 10 55.9
10 2.6 72.8 9.1 14 64.3
11 0.3 64.2 2.1 11 42.7
12 4 132.2 11.2 23 76.7
13 0.8 58.6 6 14 22.8
14 3.5 174.6 12.7 26 117.1
15 10.2 263.5 15.6 34 146.7
16 3 79.3 8.9 15 29.9
17 0.2 14.8 0.6 2 42.1
18 0.4 73.5 5.9 11 25.3
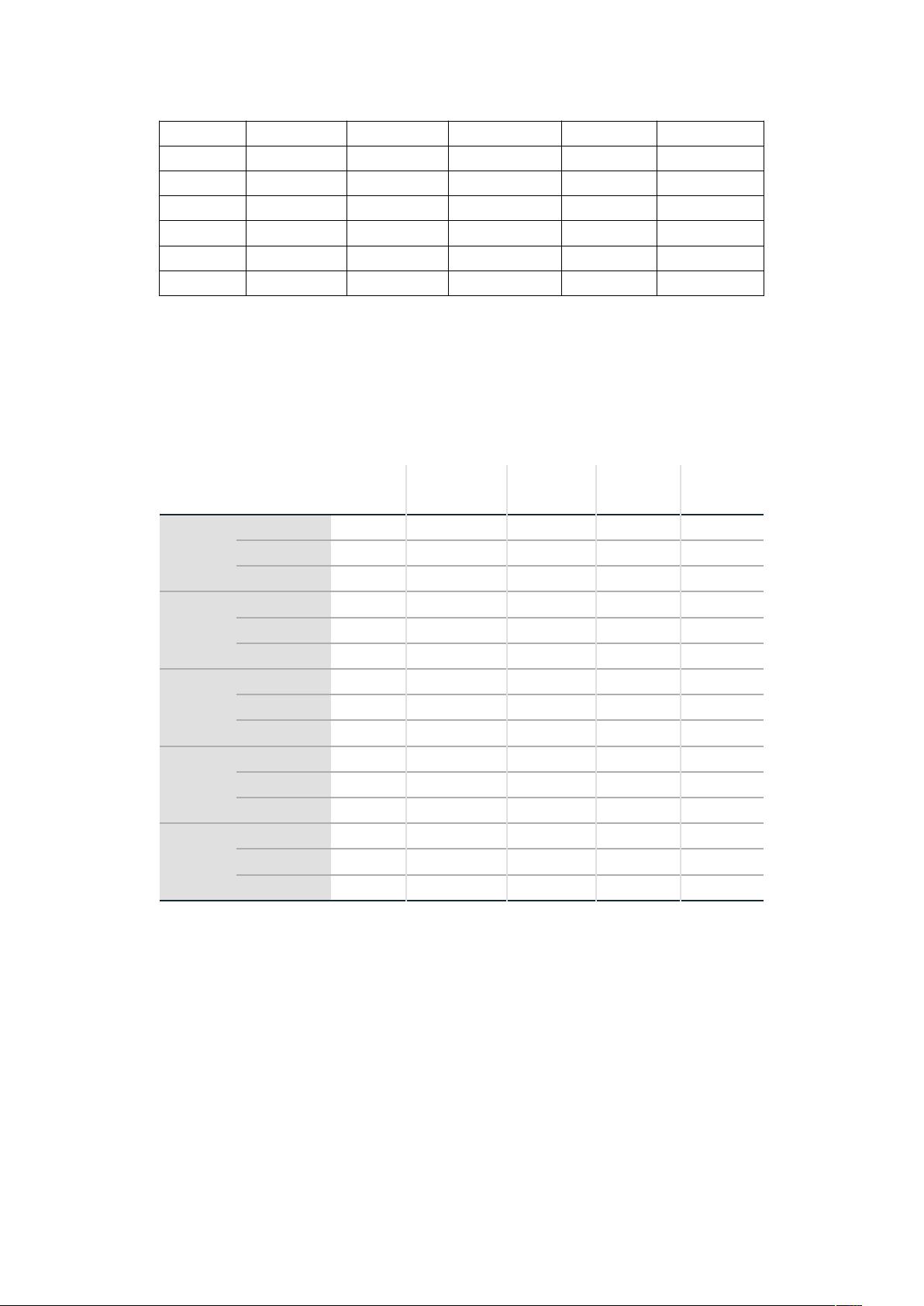
19 1 24.7 5 4 13.4
20 6.8 139.4 7.2 28 64.3
21 11.6 368.2 16.8 32 163.9
22 1.6 95.7 3.8 10 44.5
23 1.2 109.6 10.3 14 67.9
24 7.2 196.2 15.8 16 39.7
25 3.2 102.2 12 10 97.1
2、回归分析
(1)建立 y 与其余 4 个变量的简单相关系数。
相关性
不良贷款 各项贷款余额
本年累计应
收贷款
贷款项目个
数
本年固定资
产投资额
不良贷款 皮尔逊相关性
1 .844
**
.732
**
.700
**
.519
**
Sig.(双尾)
.000 .000 .000 .008
个案数
25 25 25 25 25
各 项 贷 款
余额
皮尔逊相关性
.844
**
1 .679
**
.848
**
.780
**
Sig.(双尾)
.000 .000 .000 .000
个案数
25 25 25 25 25
本 年 累 计
应收贷款
皮尔逊相关性
.732
**
.679
**
1 .586
**
.472
*
Sig.(双尾)
.000 .000 .002 .017
个案数
25 25 25 25 25
贷 款 项 目
个数
皮尔逊相关性
.700
**
.848
**
.586
**
1 .747
**
Sig.(双尾)
.000 .000 .002 .000
个案数
25 25 25 25 25
本 年 固 定
资 产 投 资
额
皮尔逊相关性
.519
**
.780
**
.472
*
.747
**
1
Sig.(双尾)
.008 .000 .017 .000
个案数
25 25 25 25 25
**. 在 0.01 级别(双尾),相关性显著。
*. 在 0.05 级别(双尾),相关性显著。
由相关性表可知相关系数矩阵为
r=
(
1 0.844
0.844 1
0.732 0.700 0.519
0.679 0.848 0.780
0.732 0.679
0.700 0.848
0.519 0.780
1 0.586 0.472
0.586 1 0.747
0.472 0.747 1
)
,故 y 与其余
4 个变量的简单相关系数分别为 0.844,0.732,0.700,0.519
(2) 建立不良贷款 y 对 4 个自变量的线性回归方程,所得的回归系数是否合
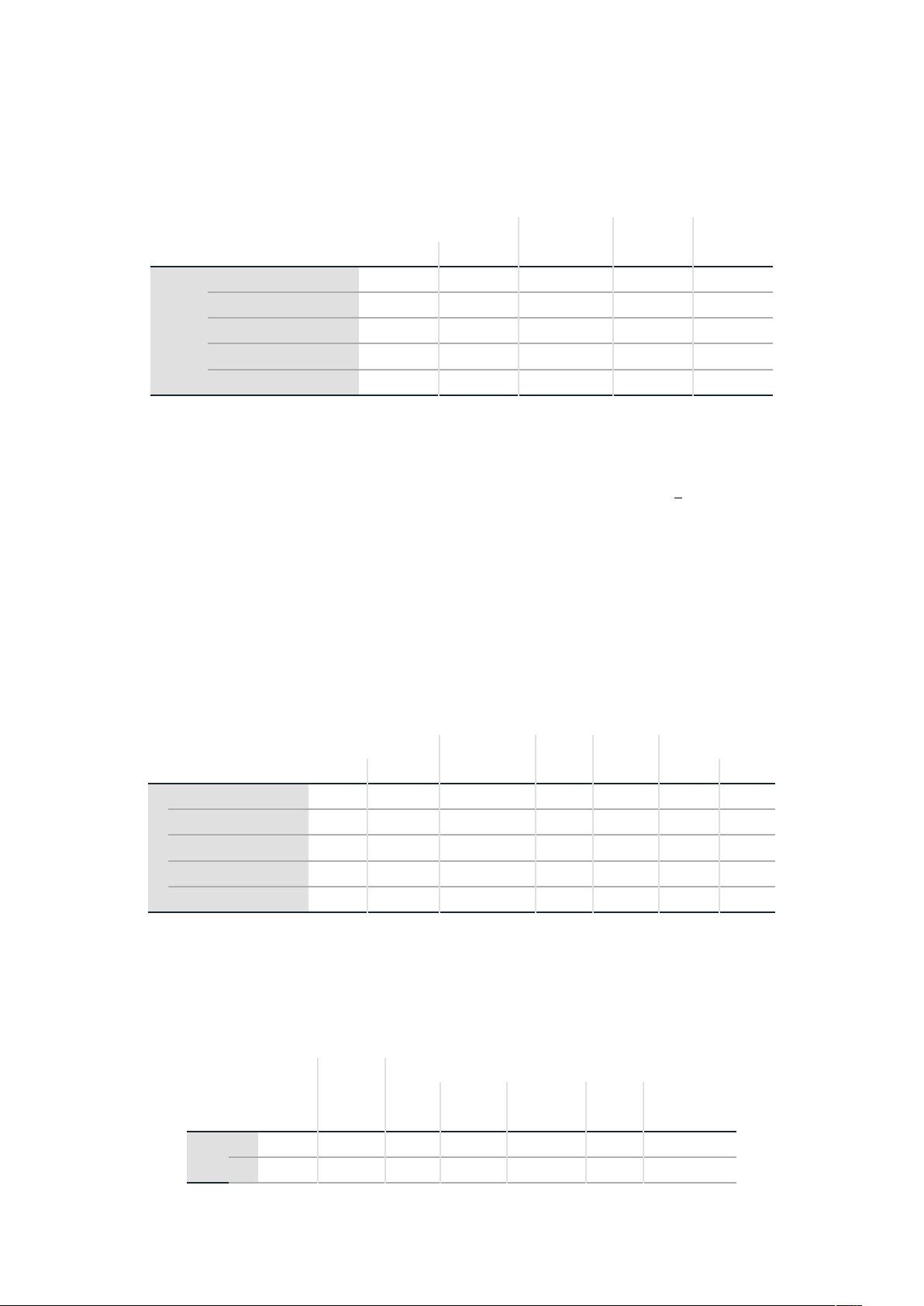
理?
系数
a
模型
未标准化系数 标准化系数
t
显著性
B
标准错误
Beta
1
(常量)
-1.022 .782 -1.306 .206
各项贷款余额
.040 .010 .891 3.837 .001
本年累计应收贷款
.148 .079 .260 1.879 .075
贷款项目个数
.015 .083 .034 .175 .863
本年固定资产投资额
-.029 .015 -.325 -1.937 .067
a. 因变量:不良贷款
由系数表可知
β
0
=− 1.022, β
1
=0.040 , β
2
=0.148 , β
3
=0.015 , β
4
=− 0.029
,所以可得
线性回归方程为
^
y=− 1.022+0.04 x
1
+0.148 x
2
+0.015 x
3
− 0.029 x
4
.
取显著性水平
α=0.05
,自由度为 n-2=25-2=23,查 t 分布表得临界值
t
α
2
(
23
)
=2.069
,由|
t
2
|=1.879<2.069 可知,应该接受原假设
H
0
: β
2
=0
,认为
β
2
不显著;由|
t
3
|
=0.175<2.069 可知,应该接受原假设
H
0
: β
3
=0
,认为
β
3
不显著;由|
t
4
|=1.937<2.069 可
知,应该接受原假设
H
0
: β
4
= 0
,认为
β
4
不显著,因变量 y 对自变量
x
2
, x
3
, x
4
的线性回
归不成立,即未通过 t 检验,回归系数不合理。
(3) 分析回归模型的共线性。
a.方差扩大因子法判断共线性
系数
a
模型
未标准化系数 标准化系数
t
显著性
共线性统计
B
标准错误
Beta
容差
VIF
1
(常量)
-1.022 .782 -1.306 .206
各项贷款余额
.040 .010 .891 3.837 .001 .188 5.331
本年累计应收贷款
.148 .079 .260 1.879 .075 .529 1.890
贷款项目个数
.015 .083 .034 .175 .863 .261 3.835
本年固定资产投资额
-.029 .015 -.325 -1.937 .067 .360 2.781
a. 因变量:不良贷款
由系数表中方差扩大因子 VIF 均小于 10,可认为自变量之间不存在严重的多重共
线性。
b.特征根判定法判断共线性
共线性诊断
a
模型 维 特征值 条件指标
方差比例
(常量)
各项贷款
余额
本年累计
应收贷款
贷款项
目个数
本年固定资
产投资额
1 1 4.538 1.000 .01 .00 .01 .00 .00
2 .203 4.733 .68 .03 .02 .01 .09
剩余12页未读,继续阅读
weixin_48894195
- 粉丝: 108
- 资源: 18
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功


评论10