
大学数学实验
Mathematical Experiments
实验4 常微分方程数值解

为什么要学习微分方程数值解
• 微分方程是研究函数变化规律的重要工具,有着广泛
的应用。如:
物体的运动, 电路的电压, 人口增长的预测
• 许多微分方程没有解析解,数值解法是求解的重要手
段,如

实验4的基本内容
3. 实际问题用微分方程建模,并求解
2. 龙格-库塔方法的MATLAB实现
*4. 数值算法的收敛性、稳定性与刚性方程
1. 两个最常用的数值算法:
• 欧拉(Euler)方法
• 龙格-库塔(Runge-Kutta)方法

实例1 海上缉私
海防某部缉私艇上的雷达发现正东方向c海里处有一艘走私船正
以速度a向正北方向行驶,缉私艇立即以最大速度b(>a)前往拦
截。如果用雷达进行跟踪时,可保持缉私艇的速度方向始终指
向走私船。
• 建立任意时刻缉私艇位置及
航线的数学模型,并求解;
• 求出缉私艇追上走私船的时间。
a
北
b
c
艇 船
实例1 海上缉私
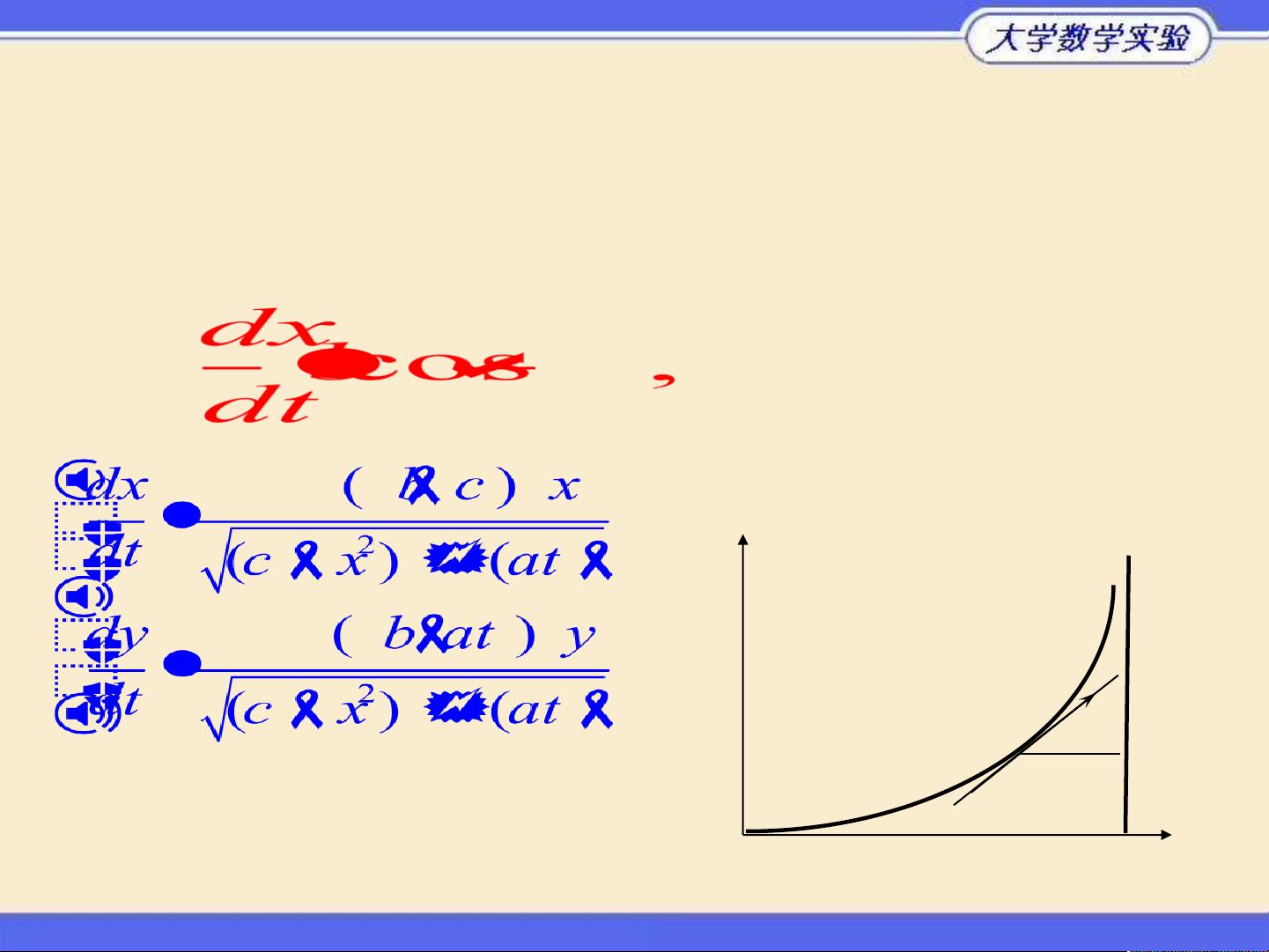
建立坐标系如图: t=0 艇在(0, 0), 船在(c, 0); 船速a, 艇速b
时刻 t 艇位于P(x, y), 船到达 Q(c, at)
模型:
0
y
x
c
R(c,y )
�
Q(c,at
)
P(x,y
)
b
由方程无法得到x(t), y(t)的解析解
需要用数值解法求解

















