2017 级数值分析第二次作业(非线性方程求根)
班级
学号
姓名
一 (20 分)用二分法求方程
3
( ) 1 0f x x x= - - =
在区间[1.0, 1.5]内的一个实根，且
要求有 3 位有效数字。试完成：
(1) 估计需要二分的次数；(8 分)
解：容易知道方程在[1.0, 1.5]有且仅有一个实根。记此实根为
*x
，根据二分法误差估
计公式有
(2)
1 2
( ) 1
*
2 2
k
k k
b a
x x
+ +
-
- £ =
(3) 要使得近似解有 3 位有效数字，只需要有
(4)
2
2
1 1
10
2 2
k
-
+
£ ´
(5) 从而可得
6k ³
，即满足精度要求的二分次数为 6 次。
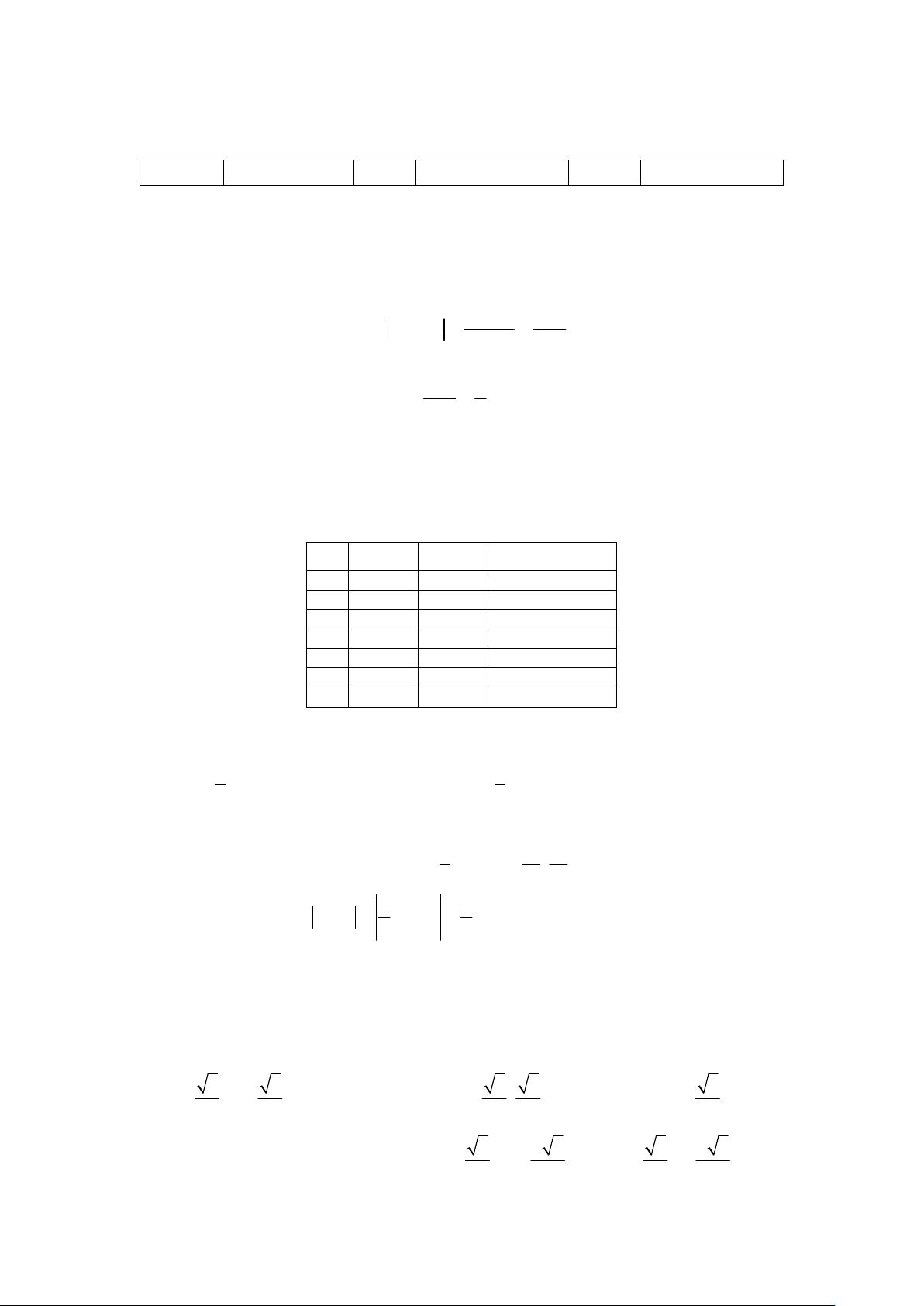
(2) 将计算过程中数据填入表 1.(中间过程填写到小数点后面 3 位)(12 分，每个
k
x
得 2 分，其它空不计分)
表 1 题 1 计算过程
k
k
a
k
b
k
x
0
1.0
1.5
1.25
1
1.25
1.5
1.375
2
1.25
1.375
1.316
3
1.313
1.375
1.349
4
1.313
1.344
1.328
5
1.313
1.328
1.320
6
1.320
1.328
1.324
二. (10 分) 为了计算方程
( ) 3 sin 2 12 0f x x x= - - =
的根，某同学将
( ) 0f x =
改写
为
1
4 sin 2
3
x x= +
，并建立迭代公式
1
1
4 sin 2
3
k k
x x
+
= +
。请问此迭代公式在 R 上是
否全局收敛的吗？说明理由。
证明：(1) 对任意的
x RÎ
，有
1 11 13
( ) 4 sin 2 ,
3 3 3
x x R
j
é ù
= + Î Í
ê ú
ë û
；
(2) 对任意的
x RÎ
，有
2 2
'( ) cos 2 1
3 3
x x
j
= £ <
;
从而可知，迭代格式在
R
上全局收敛。
三. (20 分)设有方程
3
( ) 1 0f x x x= - - =
，试回答下列问题：
(1) 确定方程
3
( ) 1 0f x x x= - - =
实根的数目；(4 分)
解：由
2
'( ) 3 1f x x= -
可知函数
3
( ) 1f x x x= - -
的单调递增区间是
3 3
, ,
3 3
æ ö æ ö
-¥ - È +¥
ç ÷ ç ÷
ç ÷ ç ÷
è ø è ø
，单调递减区间是
3 3
,
3 3
æ ö
-
ç ÷
ç ÷
è ø
。容易知道，
3
3
x = ±
是函数
3
( ) 1f x x x= - -
的两个极值点。再根据
3 2 3 3 2 3
1 1 0
3 9 3 9
f f
æ ö æ ö
= - - < - = - <
ç ÷ ç ÷
ç ÷ ç ÷
è ø è ø
，
资源评论
