Resolutionlimitoflabel-freefar-fieldmicroscopy资源-CSDN文库

93 浏览量 2021-01-26 16:00:32 上传评论收藏 793KB PDF 举报

资源推荐

资源详情

资源评论

Resolution limit of label-free far-field microscopy

Evgenii Narimanov*

Purdue University, School of Electrical Engineering, Birck Nanotechnology Center, West Lafayette, Indiana, United States

Abstract. The Abbe diffraction limit, which relates the maximum optic al reso lution to the numerical aperture of

the lenses involved and the optical wavelength, is generally considered a practical limit that cannot be

overcome with conventional imaging systems. However, it does not represent a fundamental limit to

optical resolution, as demonstrated by several new imaging techniques that prove the possibility of finding the

subwavelength information from the far field of an optical image. These include super-resolution fluorescence

microscopy, imaging systems that use new data processing algorithms to obtain dramatically improved

resolution, and the use of super-oscillating metamaterial lenses. This raises the key questi on of whether

there is in fact a fundamental limit to the optical resolution, as opposed to practical limitations due to

noise and imperfections, and if so then what it is. We derive the fundamental limit to the resolution of

optical imaging and demonstrate that while a limit to the resolution of a fundamental nature does exist,

contrary to the conventional wisdom it is neither exactly equal to nor necessarily close to Abbe’s estimate.

Furthermore, our approach to imaging resolution, which combines the tools from the physics of wave

phenomena and the methods of information theory, is general and can be extended beyond optical

microscopy, e.g., to geophysical and ultrasound imaging.

Keywords: imaging; super-resolution.

Received Sep. 17, 2019; accepted for publication Oct. 15, 2019; published online Nov. 1, 2019.

production of this work in whole or in part requires full attribution of the original publication, including its DOI.

[DOI: 10.1117/1.AP.1.5.056003]

1 Introduct ion

High-resolution optical imaging holds the key to the under-

standing of fundamental microscopic processes both in nature

and in artificial systems—from the charge carrier dynamics

in electronic nanocircuits

to the biological activity in cellular

structures.

However, optical diffraction prevents the “squeez-

ing” of light into dimensions much smaller than its wavelength,

leading to the celebrated Abbe diffraction limit.

4–7

This does not

allow a straightforward extension of the conventional optical

microscopy to the direct imaging of such subwavelength struc-

tures as cell membranes, individual viruses, or large protein

molecules. As a result, recent decades have seen an increasing

interest in developing “super-resolution” optical methods that

allow to overcome this diffraction barrier—i.e., near-field opti-

cal microscopy,

structured illumination imaging,

metamateri-

als-based super-resolution,

two-photon luminescence and

stimulated emission-depletion microscopy,

stochastic optical

reconstruction imaging,

and photoactivated localization

microscopy.

In particular, there is an increasing demand for the approach

to optical imaging that is inherently label-free and does not rely

on fluorescence, operates on the sample that is in the far field of

all elements of the imaging syst em, and offers resolution com-

parable to that of fluorescent microscopy. Although seemingly a

tall order, this task has recent ly found two possible solutions that

approach the problem from the “hardware” and “algorithmic”

sides, respectively. The former approac h relies on the phenom e-

non of “super-oscillations”—where the band-limited function

can and—when properly designed—does oscillate faster than

its fastest Fourier component. The super-oscillatory lenses that

implement this behavior have been designed and fabricated,

14,15

and optical resolution exceeding the conventional Abbe limit

has been demonstrated in experiment.

The second app roach

relies on methods of processing the “diffraction-limited” data,

taking full advantage of the fact that actual targets (and espe-

cially biological samples) are often inherently sparse.

The re-

sulting resolution improvement beyond the Abbe limit, due to

this improved data processing, has been demonstrated both in

numerical simulations and in experiment.

16–18

Far-field optical resolution beyond the Abbe limit in a scat-

tering rather than fluorescence-based approach, observed in

*Address all correspondence to Evgenii Narimanov, E-mail: evgenii@purdue.edu

Research Article

Advanced Photonics 056003-1 Sep∕Oct 2019

•

Vol. 1(5)

Refs. 14–19, clearly demonstrates that Abbe’s bound of half-

wavelength (and its quarter-wavelength counterpart for struc-

tured illumination) is not a fundamenta l limit for optical imag-

ing. This raises the key question of whether there is in fact a

fundamental bound to the optical resolution—as opposed to

practical limitations due to detector noise, imaging system im-

perfections, data processing time limits in the case when image

reconstruction corresponds to an NP-complete problem, etc.

Furthermore, the knowledge of the corresponding fundamental

limit, if such exists, and the physical mechanism behind it would

help find the way to the system that offers the optimal perfor-

mance—just as deeper understanding of thermodynamics and

Carnot’s limit helped the design of practical heat engines.

In this work, we show that there is in fact a fundamental limit

on the resolution of far-field optical imaging, which is however

much less stringent than Abbe’s criterion. The presence of any

finite amount of noise in the system, regardless of how small its

intensity, leads to a fundamental limit on the optical resolution,

which can be expressed in the form of an effective uncertainty

relation. This limit has an essential information-theoretical

nature and can be connected to the Shannon’s theory of infor-

mation transmission in linear systems.

2 Definition of the Resolution Limit

We define the diffraction limit Δ as the shortest spatial scale of

the object whose geometry can still be reconstructed, error-free,

from the far-field opti cal measurements in the presence of noise.

(Although the concept o f error-free information recovery in the

presence of noise may sound surprising, it lies in the heart of

modern computer networks where terabytes of data are trans-

ferred error-free over noisy transmission lines.) Without loss

of generality, one can then assume that the object is composed

of an arbitrary numbe r of point scatterers of arbitrary amplitudes

located at the nodes of the grid with the period Δ, as any addi-

tional structure in the sources (or scatterers) or variations in po-

sition will add to the information that needs to be recovered

from far-field measurement for the successful reconstruction

of the geometry of the object. (For a given illumination field,

each point scatterer can be treated as an effective point source .)

Furthermore, the essential “lower bound” nature of Δ further

allows to reduce the problem to that of an effectively one-dimen-

sional target (formed by line, rather than point, sources)—since,

as was already known to André

and Rayleigh,

line sources

are more easily resolvable than point sources.

To calculate the fundamental resolution limit, it is therefore

sufficient to consider the model system of an array of line

“sources” of arbitrary (including zero) amplitudes, located at

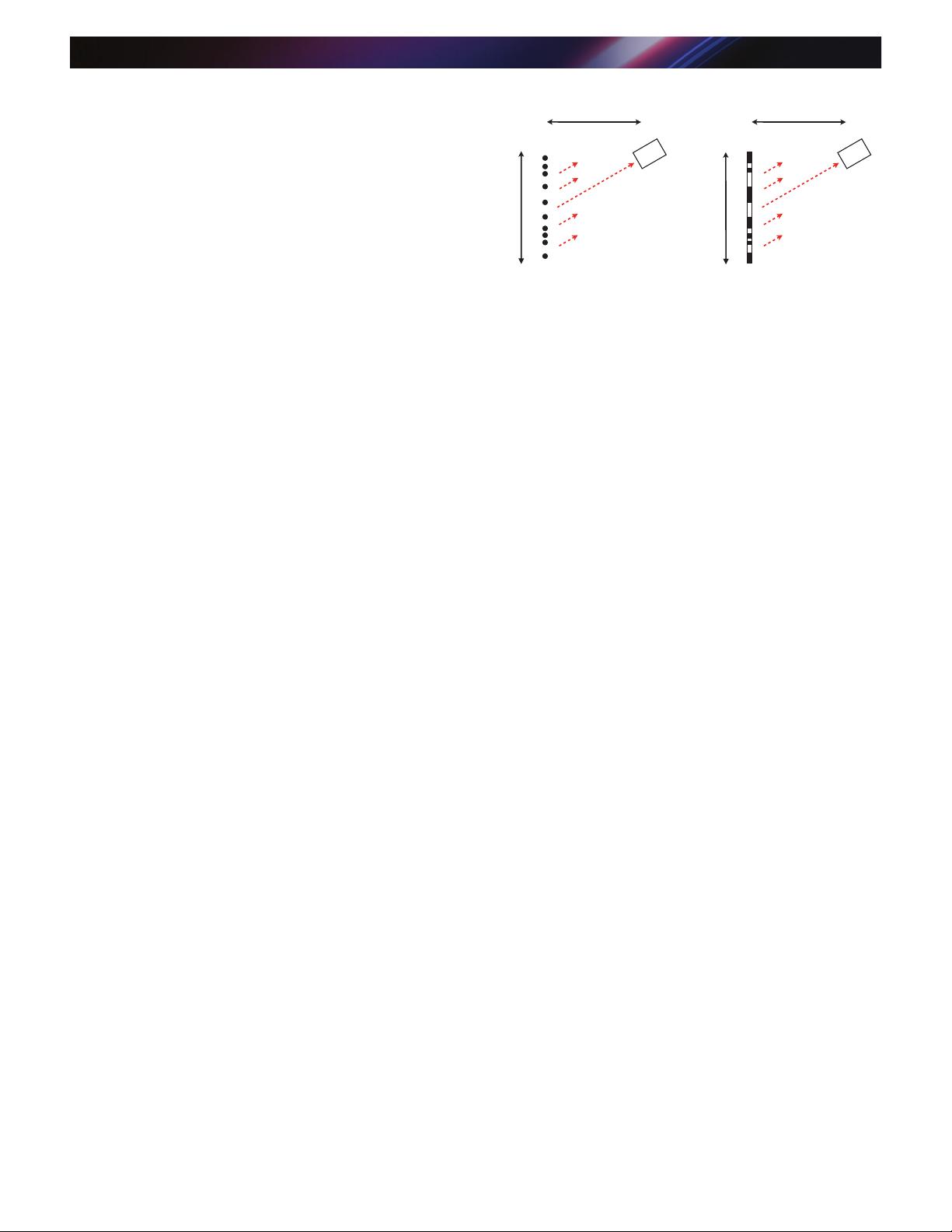
the node points of the grid with the period Δ [see Fig. 1(a)].

Note that in terms of the information that is detected in the far

field and the information that is necessary and sufficient for the

target reconstruction, this problem is identical to that of a step

mask where thickness and/or permittivity changes at the nodes

of the same grid by the amounts proportional to the amplit udes

of the corresponding line sources (as the point source distribu-

tion corresponds to the spatial derivative of the mask “profile”)

[see Fig. 1(b)].

Note that the reduction of the original problem to that of an

effectively one-dimensional profile is not a simplification for the

sake of convenience or reduction of the mathematical complex-

ity. It is exactly this “digitized” one-dimensional profile that cor-

responds to the smallest “resolvable” spatial scale among all

objects with a low bound on their spatial variations and therefore

defines the fundamental resolution limit. Furthermore, in many

cases, the actual object is formed by two (or more) materials that

form sharp interfaces. In this case, the step mask that is equiv-

alent to our point source model offers an adequate representa-

tion of the actual target.

However, even within the original framework of “resolving”

two point sources,

the result clearly depends on the difference

of their amplitudes—with increasing disparity between the two

leading to progressively worse “resolution.” The “ultimate” res-

olution limit Δ, therefore, corresponds to the case of identical

point sources (or subwavelength scatterers), which are present

only in an (unknown) fraction of the grid nodes. Note that such a

digital mask corresponds to the common case of a pattern

formed by a single material (e.g., the surrounding air) [see

Fig. 1(b)].

When the distance to the detector R is much larger than the

aperture L, R ≫ L (see Fig. 1), for the far-field signal detected

in the given polarization and in the direction defined by the

wavevector k (see Fig. 1 and Sec. 7):

sðkÞ¼

ðρ

Þexpðik · ρ

ÞþnðkÞ; (1)

where E

is the incident field “illuminating” the target, i is the

(integer) index that labels the (point) scatterers with the corre-

sponding polarizabilities α

, ρ

≡ ðx

Þ, k ≡ ðk

Þ is the

wavevector with the magnitude jkj¼ω∕c ≡ k

, ω is the light

frequency, and c is the speed of light (in the medium surround-

ing the target). Here nðkÞ corresponds to the effective noise,

which includes the contributions from all origins (detector dark

currents, illumination field fluctuations, etc.). Using data for im-

aging with different electromagnetic field polarizations, the ef-

fective noise can be correspondingly reduced.

Equivalently, for the case of the object in the form of a (di-

electric) mask [see Fig. 1(b)], we obtain

sðkÞ¼

ρΔϵðρÞE

ðρ

Þexpðik · ρ

ÞþnðkÞ; (2)

where Δϵ is the difference between the dielectric permittivities

of the object and the background.

Note that Eqs. (1) and (2) are linear in Δϵ and α (see Sec. 7),

which physically correspond to the limit when multiple scatter-

ing is weak . Although this is generally the case in optical

(a)

(b)

Fig. 1 The schematic representation of the imaging set-up, for

the object formed by (a) an array of small particles/lines and

(b) a (binary) mask. D labels the position of a (coherent) detector,

L is the size of the object (and equivalently the imaging aperture),

and R is the distance from the object to the detector; in the far

field R ≫ L.

Narimanov: Resolution limit of label-free far-field microscop y

Advanced Photonics 056003-2 Sep∕Oct 2019

•

Vol. 1(5)

剩余6页未读，继续阅读

评论收藏

内容反馈

weixin_38692122

粉丝: 13
资源: 960

Resolution limit of label-free far-field microscopy

Resolution-enhanced intensity diffraction tomography in high numerical aperture label-free microscopy

Near field microscopy and near field optics英文书籍

2017-OC-ISM径向偏振-Image-scanning-microscopy-with-radially-polarized-l.pdf

dicom-microscopy-viewer：基于Web的DICOM可见光整个幻灯片显微镜图像查看器

PyPI 官网下载 | MicroscoPy-0.9-py2-none-any.whl

Phase-shifting-free resolution enhancement in digital holographic microscopy under structured illumination

Five-wavelength optical-resolution photoacoustic microscopy of blood and lymphatic vessels

Static recording characteristics of new type super-resolution near-field structure

python-microscopy：python-microscopy环境-用于光学显微镜的开源软件包

near field optical microscopy and spectroscopy with pointed probes

Editorial — Introduction to the special issue on super-resolution optical microscopy

Advancing biological super-resolution microscopy through deep l

scanning electron microscopy and x-ray microanalysis 4th

Disclosing transverse spin angular momentum of surface plasmon polaritons through independent spatiotemporal imaging of its in-plane and out-of-plane electric field components

Advancing biological super-resolution microscopy throu

小波图像分割matlab代码-Microscopy-Codes:显微镜代码

Optical-resolution photoacoustic microscopy continually monitors macrophages activities of acute inflammation

Coherent optical adaptive technique improves the spatial resolution of STED microscopy in thick samples

3D depth-coded photoacoustic microscopy with a large field of view for human skin imaging

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

最新资源

Qt 5实现串口调试助手（源工程文件、0积分下载）