考虑多约束的混合流水车间MOJ调度

多品种|换模时间|析取网络流|改进型列生成

30 浏览量 2021-01-13 20:55:23 上传评论收藏 234KB PDF 举报

资源推荐

资源详情

资源评论

第 31 卷第 5 期

Vol. 31 No. 5

控制与决策

Control and Decision

2016 年 5 月

May 2016

考虑多约束的混合流水车间 MOJ 调度

文章编号: 1001-0920 (2016) 05-0776-07 DOI: 10.13195/j.kzyjc.2015.0399

周炳海, 王腾

(同济大学机械与能源工程学院，上海 201804)

摘要: 考虑晶圆加工过程中的多品种和与次序相关的换模时间约束, 以系统总完工时间最小为优化目标, 建立混

合流水车间 MOJ 调度模型. 在此基础上, 提出了基于作业-产品-机器三层析取网络流的列生成算法. 为进一步改善列

生成算法存在的尾效应, 将基于次梯度优化的拉格朗日松弛算法嵌入列生成算法框架中, 构建了采用双重迭代的改

进型列生成 (MCG) 算法. 最后, 通过理论分析和仿真实验表明了 MCG 算法是有效、可行的.

关键词: 多品种；换模时间；析取网络流；改进型列生成

中图分类号: TP391 文献标志码: A

Scheduling multiple orders per job with various constraints for hybrid

ﬂow shop

ZHOU Bing-hai, WANG Teng

(School of Mechanical Engineering ，Tongji University，Shanghai 201804，China．Correspondent：ZHOU Bing-hai,

E-mail：bhzhou@tongji.edu.cn)

Abstract: With a comprehensive consideration of multiple product types and sequence-dependent setup times constraints

in which processes of wafer fabrications, a scheduling model of multiple orders per job(MOJ) in a hybrid ﬂow shop with an

objective function of minimizing total completion time of the system is developed. On the basis of the descriptions, a column

generation algorithm based on the job-product-machine three level disjunctive network ﬂow is proposed. Furthermore, to

improve the degradation effects of column generation algorithm, Lagrangian relaxation with sub-gradient optimization is

combined into the frame of column generation algorithm, and then a modiﬁed column generation(MCG) algorithm adopting

dual iteration is proposed. Finally, theory analysis and simulation experiments show that the developed MCG algorithm is

valid and feasible.

Keywords: multiple product types；setup times；disjunctive network ﬂow；modiﬁed column generation

0 引引引言言言

单作业多订单 (MOJ) 调度问题

[1]

作为对半导体

生产线的高效运行带来重要影响的 NP-hard 问题

[2]

近年来受到了业界和学术界越来越多的关注. 为有

效解决单机 MOJ 调度问题, 学者们提出了多种调度

方法. 文献 [2-4] 对不考虑订单准备时间等因素的理

想化单机 MOJ 调度问题进行了基于智能搜索算法的

求解研究. Sarin 等

[5]

基于对理想化单机 MOJ 问题分

析得到的性质定理, 提出了较传统整数规划模型更

为有效的精确算法来求解中小规模 MOJ 调度问题.

Mason 等

[6]

提出的启发式算法对订单规模数为 100

以上甚至达到 10 000 的超大规模单机 MOJ 调度问题

进行了有效求解. Jampani 等

[7]

对带准备时间的单机

MOJ 调度问题, 构造了列生成启发式算法.

随着对单机 MOJ 问题研究的日趋完善, 对于多

机 MOJ 调度问题的延伸探讨也开始受到重视. Laub

等

[8]

和 Sarin 等

[9]

对双机流水线车间 MOJ 调度问题,

构建了启发式算法进行有效求解. Jampani 等

[7]

和 Jun

等

[10]

对考虑订单到达时间的并行机 MOJ 调度问题,

提出了有效的启发式算法进行求解. Chen

[11]

对考虑

多品种、与次序相关的换模时间的流水线车间 MOJ

调度问题, 建立了混合整数规划模型, 但未对大规模

的 MOJ 调度进行调度方法研究.

目前较少见到有关多品种 MOJ 调度问题的报道.

现有的诸多解决单一产品加工背景下的调度方法不

能直接推广到多品种问题中.

收稿日期: 2015-04-01；修回日期: 2015-06-28.

基金项目: 国家自然科学基金项目(61273035, 71471135).

作者简介: 周炳海(1965−), 男, 教授, 博士生导师, 从事制造系统的建模、调度等研究；王腾(1988−), 男, 硕士生, 从事

制造系统调度算法的研究.

第 5 期

周炳海等: 考虑多约束的混合流水车间 MOJ 调度

777

本文研究的混合流水车间 MOJ 调度问题以最小

化总完工时间为目标函数, 同时考虑订单品种的多样

性和与次序相关换模时间的约束. 最后通过理论分析

和仿真实验表明了 MCG 算法的有效性和可行性.

1 问问问题题题描描描述述述

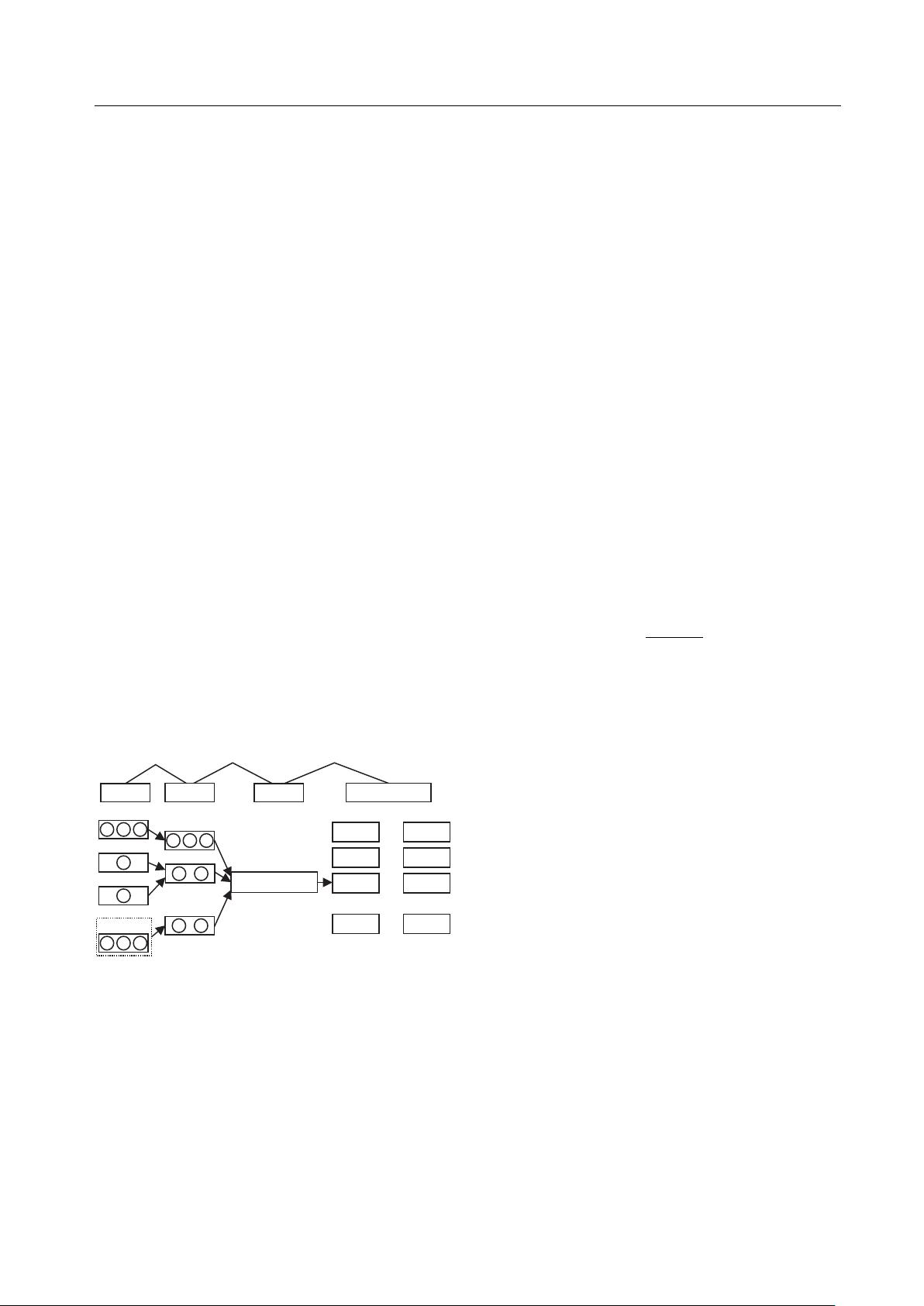
混合流水车间 MOJ 调度问题见图 1. 首先将 𝑛 个

订单 (𝑂

, 𝑂

, ⋅ ⋅ ⋅ , 𝑂

𝑛

) 成组分配到 𝑚 个作业 (𝐽

, 𝐽

⋅ ⋅ ⋅ , 𝐽

𝑚

) 中, 再将 𝑚 个作业排序成 (𝐽

, 𝐽

, ⋅ ⋅ ⋅ , 𝐽

𝑚

⋅ ⋅ ⋅ , 𝐽

) 进入混合流水车间的 𝑃 道工序流水加工, 每

道工序上有 𝑀

𝑝

⩾ 1 (𝑝 ∈ {1, 2, ⋅ ⋅ ⋅ , 𝑃 }) 台同速并行机

且至少有一道工序的机器台数不少于 2 台.

为有效地描述混合流水车间 MOJ 调度问题, 作

如下假设: 1) 订单的调度需保持完整性; 2) 每个订单

只含有一种产品; 3) 每个作业只含有产品种类相同的

订单; 4) 每一个作业中载有的晶圆个数不能超过其承

载上限 𝐾; 5) 参与调度的作业非空; 6) 每道工序中, 一

个作业只能分配到任意选择的一台并行同速机; 7) 每

一台机器的同一位置上有且仅有一个作业在加工;

8) 机器在加工不同品种产品时所需的换模时间与次

序相关; 9) 机器加工同一作业到加工完成前, 不会中

断工作; 10) 同一个作业中的所有订单有相同的完工

时间; 11) 各工序的机器在 0 时刻空闲可用; 12) 所有

订单初始时刻的到达时间为 0; 13) 工序中分配到同一

机器上的作业, 按顺序加工; 14) 同一工序中的作业按

到达时间先后, 优先分配到空闲机器加工.

!"#$

%&'(

%&)*+,-

,-M

,-2

,-1

,-M

,-2

,-1

.( P

/01234

J J J J

2 3 1

, ,, ,,

...

1 1 1

2 2

1 1

...

1 1

1 1 1

...

.( 1

图 1 混合流水车间 MOJ 调度问题

由假设 1) 可知, 每一道工序中, 一个订单只能且

必须分配到一个作业和一台机器上, 有

𝑀

𝑝

∑

𝑚=1

𝜑

∑

𝑗=1

𝑋

𝑖,𝑗,𝑚,𝑝

= 1,

𝑖 = 1, 2, ⋅ ⋅ ⋅ , 𝑁, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃. (1)

其中: 𝑋

𝑖,𝑗,𝑚,𝑝

为 0-1 变量, 如果在工序 𝑝, 订单 𝑖 被分

配到机器 𝑚 上加工的作业 𝑗 中, 则其值为 1, 否则为 0;

𝑁 为订单数; 𝜑 为作业数.

由假设 2) 和假设 3) 可知, 对于不同订单, 只有当

品种相同时才能分配到同一个作业中, 即

𝑓

𝑖

𝜑

∑

𝑙=1

𝑙𝜆

𝑖𝑙

, 𝑖 = 1, 2, ⋅ ⋅ ⋅ , 𝑁; (2)

𝑓

𝑖

⩽ 𝑓

𝑖

′

+ 𝑀

big

(2 − 𝑋

𝑖,𝑗,𝑚,𝑝

− 𝑋

𝑖

′

,𝑗,𝑚,𝑝

𝑖, 𝑖

′

= 1, 2, ⋅ ⋅ ⋅ , 𝑁, 𝑖 ∕= 𝑖

′

, 𝑗 = 1, 2, ⋅ ⋅ ⋅ , 𝜙,

𝑚 = 1, 2, ⋅ ⋅ ⋅ , 𝑀

𝑝

, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃 ; (3)

𝑓

𝑖

⩾ 𝑓

𝑖

′

− 𝑀

big

(2 − 𝑋

𝑖,𝑗,𝑚,𝑝

− 𝑋

𝑖

′

,𝑗,𝑚,𝑝

𝑖, 𝑖

′

= 1, 2, ⋅ ⋅ ⋅ , 𝑁, 𝑖 ∕= 𝑖

′

, 𝑗 = 1, 2, ⋅ ⋅ ⋅ , 𝜙,

𝑚 = 1, 2, ⋅ ⋅ ⋅ , 𝑀

𝑝

, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃. (4)

其中: 𝑓

𝑖

为订单 𝑖 的产品标号, 𝜆

𝑖𝑙

为 0-1 变量, 如果订

单 𝑖 属于产品 𝑙, 则其值为 1, 否则为 0; 𝜙 为产品种类

数; 𝑀

big

为一个较大的正数.

由假设 4) 可知, 每个作业中所有订单的晶圆总

数不能超过 𝐾, 即需满足

𝑁

∑

𝑖=1

𝑛

𝑖

𝑋

𝑖,𝑗,𝑚,𝑝

⩽ 𝐾, 𝑗 = 1, 2, ⋅ ⋅ ⋅ , 𝜙,

𝑚 = 1, 2, ⋅ ⋅ ⋅ , 𝑀

𝑝

, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃, (5)

其中 𝑛

𝑖

为订单 𝑖 所含有的晶圆数.

由假设 5) 可知, 作业数需满足

𝜙 =

𝜑

∑

𝑙=1

{⌊

𝑁

∑

𝑖=1

𝑛

𝑖

𝜆

𝑖𝑙

𝐾

⌋

+ 1

}

. (6)

由假设 6) 和 7), 可得

𝜃

𝑚,𝑝

∑

𝑟=1

𝑀

𝑝

∑

𝑚=1

𝑄

𝑗,𝑚,𝑟,𝑝

= 1,

𝑗 = 1, 2, ⋅ ⋅ ⋅ , 𝜙, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃 ; (7)

𝑀

𝑝

∑

𝑚=1

𝜙

∑

𝑗=1

𝑄

𝑗,𝑚,𝑟,𝑝

= 1,

𝑟 = 1, 2, ⋅ ⋅ ⋅ , 𝜃

𝑚,𝑝

, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃. (8)

其中: 𝑄

𝑗,𝑚,𝑟,𝑝

为 0-1 变量, 如果在工序 𝑝, 作业 𝑗 被分

配到机器 𝑚 的 𝑟 位置上加工, 则其值为 1, 否则为 0;

𝜃

𝑚,𝑝

为工序 𝑝 中机器 𝑚 拥有的位置数.

基于假设 8) ∼ 假设 10) 可知, 订单 𝑖 的完工时间

为作业 𝑗 (分配有订单 𝑖) 的开始加工时间、作业 𝑗 内晶

圆的批加工时间、与次序相关的换模时间之和, 即

𝐹

𝑖,𝑗,𝑚,𝑝

= 𝜌

𝑓

𝑖

,𝑝

+ 𝑡

𝑗−1,𝑗,𝑚,𝑝

+ 𝑠

𝑖,𝑗,𝑚,𝑝

𝑖 = 1, 2, ⋅ ⋅ ⋅ , 𝑁, 𝑗 ∈ {1, 2, ⋅ ⋅ ⋅ , 𝜙},

𝑚 ∈ {1, 2, ⋅ ⋅ ⋅ , 𝑀

𝑝

}, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃. (9)

其中: 𝐹

𝑖,𝑗,𝑚,𝑝

为订单 𝑖 在工序 𝑝 的机器 𝑚 上的完工

时间; 𝜌

𝑓

𝑖

,𝑝

为 𝑓

𝑖

品种晶圆在工序 𝑝 的机器 𝑚 上的批

加工时间; 𝑡

𝑗−1,𝑗,𝑚,𝑝

为工序 𝑝 上的机器 𝑚 由加工作

业 𝑗 − 1 切换到作业 𝑗 时所需的换模时间, 需满足

𝑡

𝑗−1,𝑗,𝑚,𝑝

= 0, 𝑗 = 1 或 𝑗 > 1 且 𝑓

𝑗−1

= 𝑓

𝑗

𝑚 ∈ {1, 2, ⋅ ⋅ ⋅ , 𝑀

𝑝

}, 𝑝 = 1, 2, ⋅ ⋅ ⋅ , 𝑃 ; (10)

剩余6页未读，继续阅读

评论收藏

内容反馈

weixin_38625192

粉丝: 4
资源: 943

考虑多约束的混合流水车间MOJ 调度

最新资源

考虑多约束的混合流水车间MOJ 调度

Matlab遗传算法求混合流水车间调度最优问题

Topcoder 插件 moj

MOJ20_UML资料

moj：:fire:moj-小表情符号cli:fire:

moj

wp-moj-blocks:生成MoJ自定义古腾堡块的WordPress插件

moj-design-system:MOJ服务团队可以在这里找到英国司法部服务的样式，组成和样式

moj-botek:布莱布尔

coffee-and-coding-public:可以公开获得的MoJ咖啡和编码会议

acronyms:MoJ中使用的缩写列表及其定义

2018_moj_affiliation:法务部所属机关

mojio.pebble:Moj.io的卵石客户端

moj_elements:增加 GOVUK 元素

cloud-platform:MoJ云平台上的文档

一键装topcoder

Repl.it-URI-MOJ：打算在我学习的同时分享一些知识。 使用电子法官，OO基础知识，数据结构和复杂性

Mojio.Android:Moj.io 原生 Android 应用的原型

mojular:Bower友好的MOJ模板，样式和资产

fb-editor:MoJ在线团队的新编辑

Moj Mobility Manager-开源

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

最新资源

Repl.it-URI-MOJ：打算在我学习的同时分享一些知识。使用电子法官，OO基础知识，数据结构和复杂性

Qt 5实现串口调试助手（源工程文件、0积分下载）