格子密码1

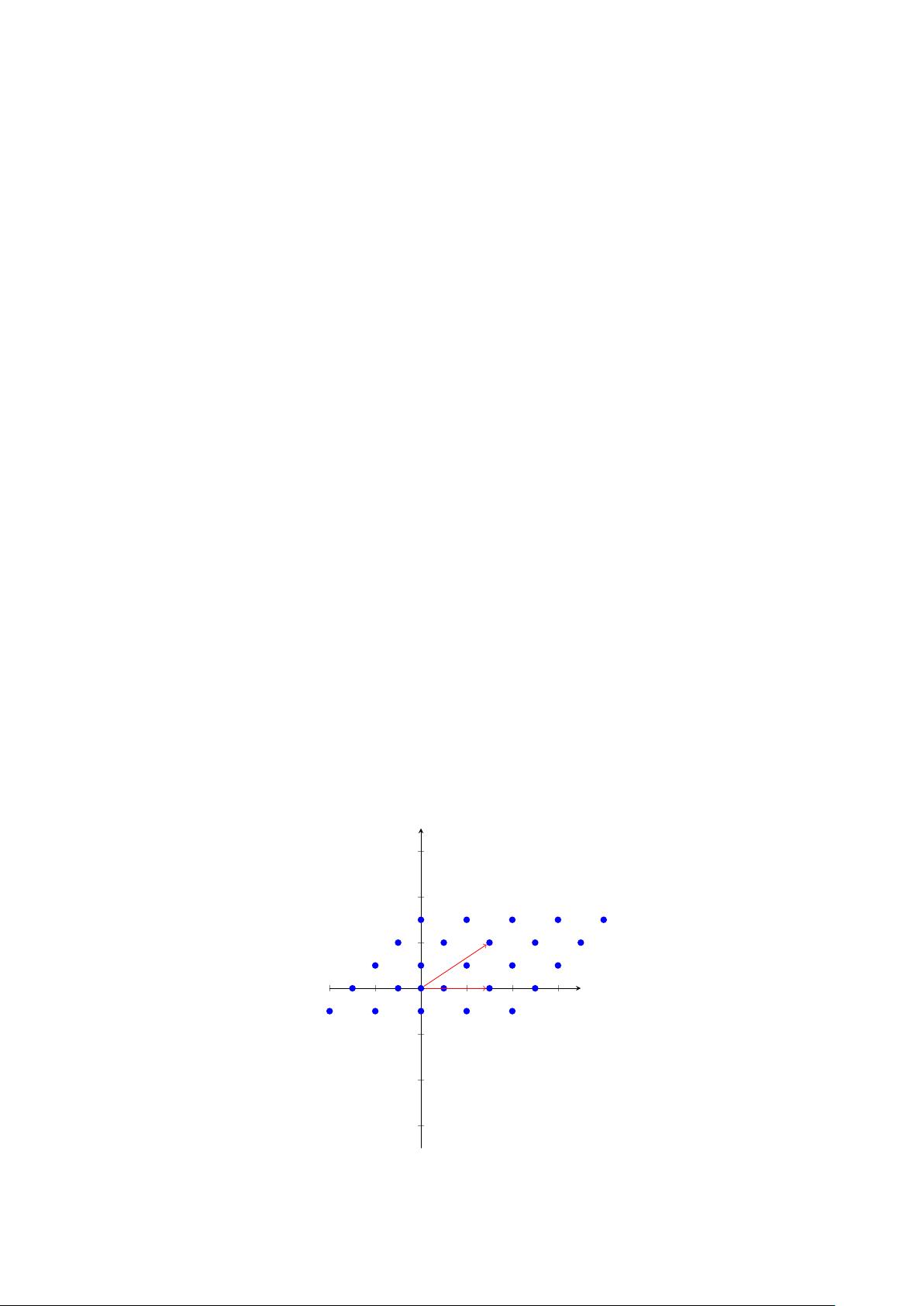
格子密码是一种基于数学中的格理论（Lattice Theory）构建的密码学方法，它在现代密码学中占有重要地位，特别是在后量子密码学领域。后量子密码学关注的是设计能够抵御未来可能出现的量子计算机攻击的加密系统。由于Shor的算法表明传统公钥密码学如RSA和ECC在量子计算面前可能不安全，基于格子的密码学成为了一个研究热点。 **格子的定义**： 在欧几里得空间R^n中，一组线性独立的向量{v1, v2, ..., vn}可以构成一个n维格L。这个格L由这些向量的整数线性组合构成，即所有形如a1v1 + a2v2 + ... + anvn的向量，其中ai都是整数。一个格的基是生成这个格的n个独立向量的任意集合，格子有无限多组基。 **基本域**： 设L是一个n维格，B={v1, v2, ..., vn}是L的一个基，L的基本域F(v1, v2, ..., vn)是所有形如t1v1 + t2v2 + ... + tnvn的向量集合，其中ti在0到1之间。基本域可以理解为格中每个向量的“最小单位”。 **格规约算法**： 格规约是找到一组基向量，使得它们具有特定的优化性质，例如是最小长度的。通常，这个过程通过格的LLL（Lenstra-Lenstra-Lovász）算法实现，它是一个迭代过程，不断调整基向量，使其满足某些条件。如例子所示，通过比较向量的长度并进行交换和调整，我们可以找到一个接近最优的基。 **最短向量问题（SVP）**： SVP是在给定的格L中找到一个非零向量，使其欧几里得范数最小。这个问题在计算上是困难的，这为基于格子的密码系统的安全性提供了基础。 **最近向量问题（CVP）**： CVP是在格L之外给定一个向量w，找到格中与w最接近的向量v。这个问题同样复杂，对于格子密码的安全性至关重要，因为它对应于解密过程中的逆运算。 **应用**： 格子密码学的应用包括公钥加密、数字签名、认证协议等。它的安全性基于解决SVP和CVP的困难性，这些问题在高维格中的计算复杂度非常高，使得破解变得极其困难。 格子密码学结合了数学的深度和计算的挑战，为构建安全的未来通信提供了坚实的基础。随着技术的发展，格子理论将继续在密码学界扮演关键角色。