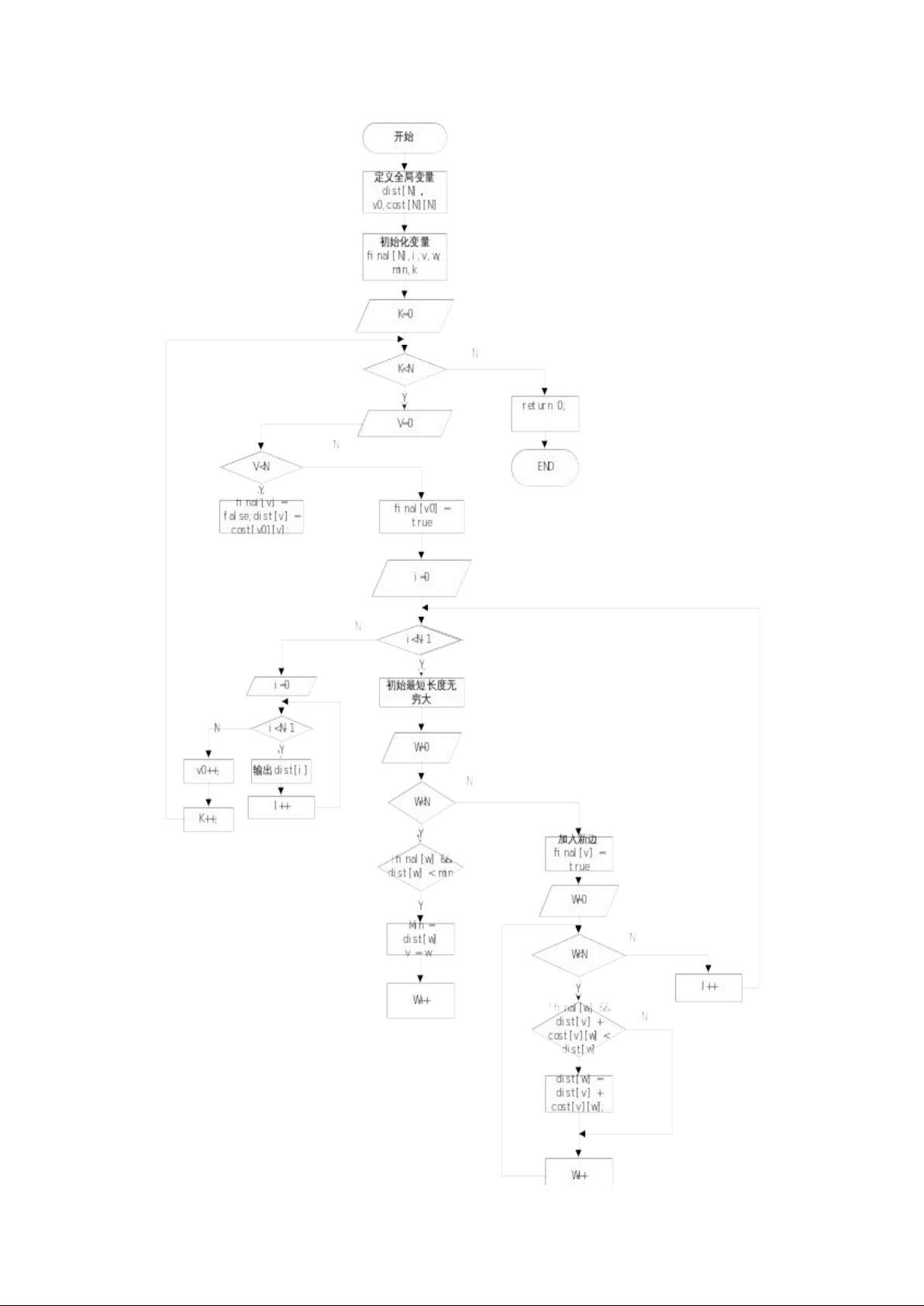
Dijkstra算法的流程图.doc

Dijkstra算法的流程图 Dijkstra算法是典型最短路算法，用于计算一个节点到其他所有节点的最短路径。其主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。 Dijkstra算法的流程图可以分为以下几个步骤： 1. 初始化：将源的距离dist[s]设为0，其他的点距离设为无穷大，同时把所有的点状态设为没有扩展过。 2. 循环n-1次： a. 在没有扩展过的点中取一距离最小的点u，并将其状态设为已扩展。 b. 对于每个与u相邻的点v，如果dist[u] + w[u,v] < dist[v]，那么把dist[v]更新成更短的距离dist[u] + w[u,v]。此时到点v的最短路径上，前一个节点即为u。 3. 结束：此时对于任意的u，dist[u]就是s到u的距离。 在实现Dijkstra算法时，我们可以使用邻接矩阵来存储图。在该程序中设置一个二维数组来存储任意两个顶点之间的边的权值。用户可以将任意一个图的信息通过键盘输入，让后在输入要查找的两个顶点，程序可以自动求出这两个顶点之间的最短路径。 在设计思想中，我们可以将源点记为s，w[u,v]为点u和v之间的边的长度，结果保存在dist[]中。然后，我们可以通过最短路径的计算，输入从任意两个顶点之间的最短路径的大小。 在程序源代码中，我们可以使用C语言来实现Dijkstra算法。我们需要定义一些常量，如true、false、I和N等。然后，我们可以定义邻接矩阵cost[N][N]，其中包含了所有顶点之间的边的权值。我们还需要定义dist[N]数组来存储当前最短路径长度。 在main函数中，我们可以使用for循环来实现Dijkstra算法的流程图。我们需要初始化最短路径长度数据，然后我们可以使用for循环来寻找最短的边，并将其状态设为已扩展。我们可以输出任意两个顶点之间的最短路径。 Dijkstra算法的流程图可以帮助我们更好地理解和实现最短路算法，从而解决复杂的图形问题。