清华大学电磁场与波教案

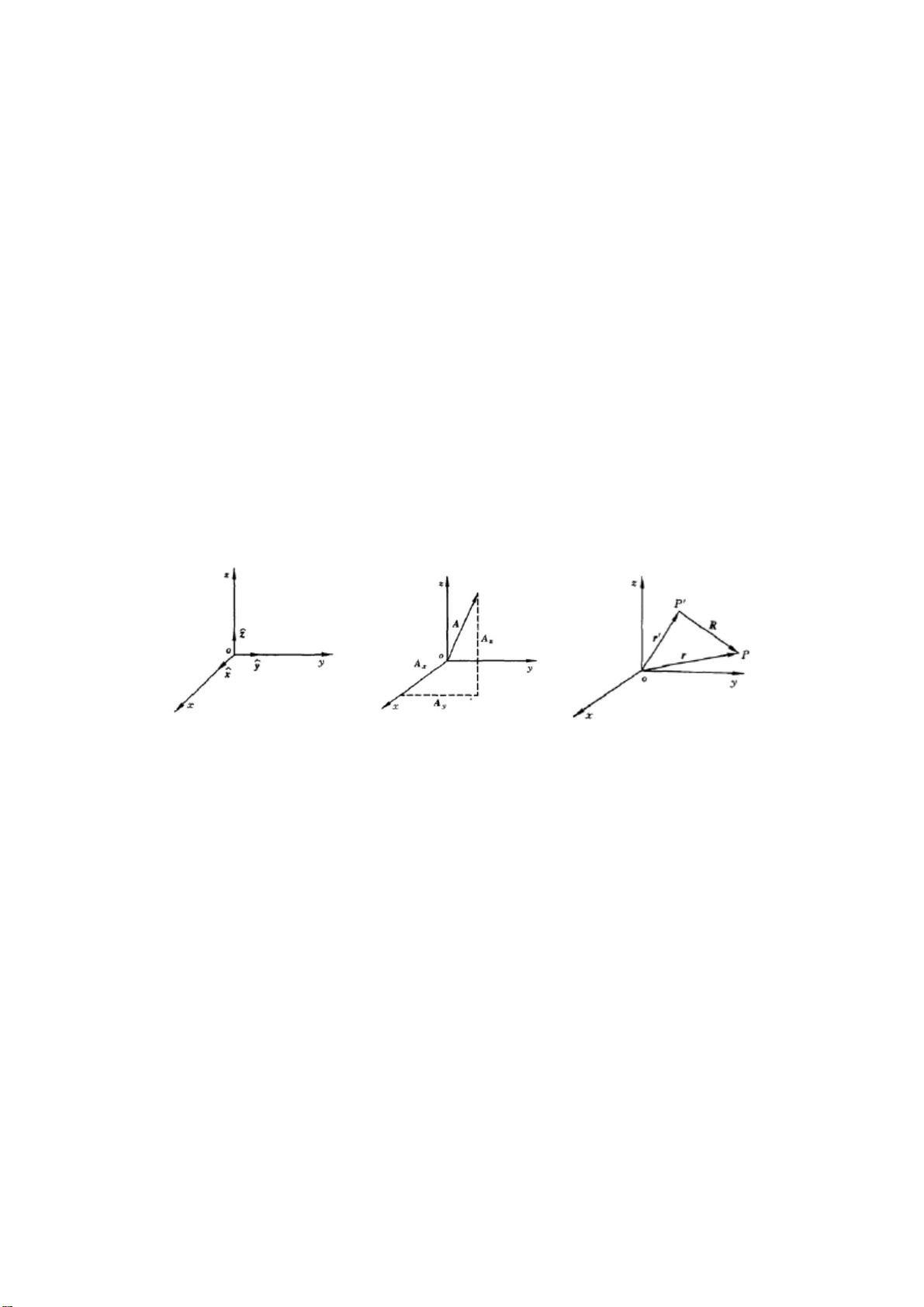
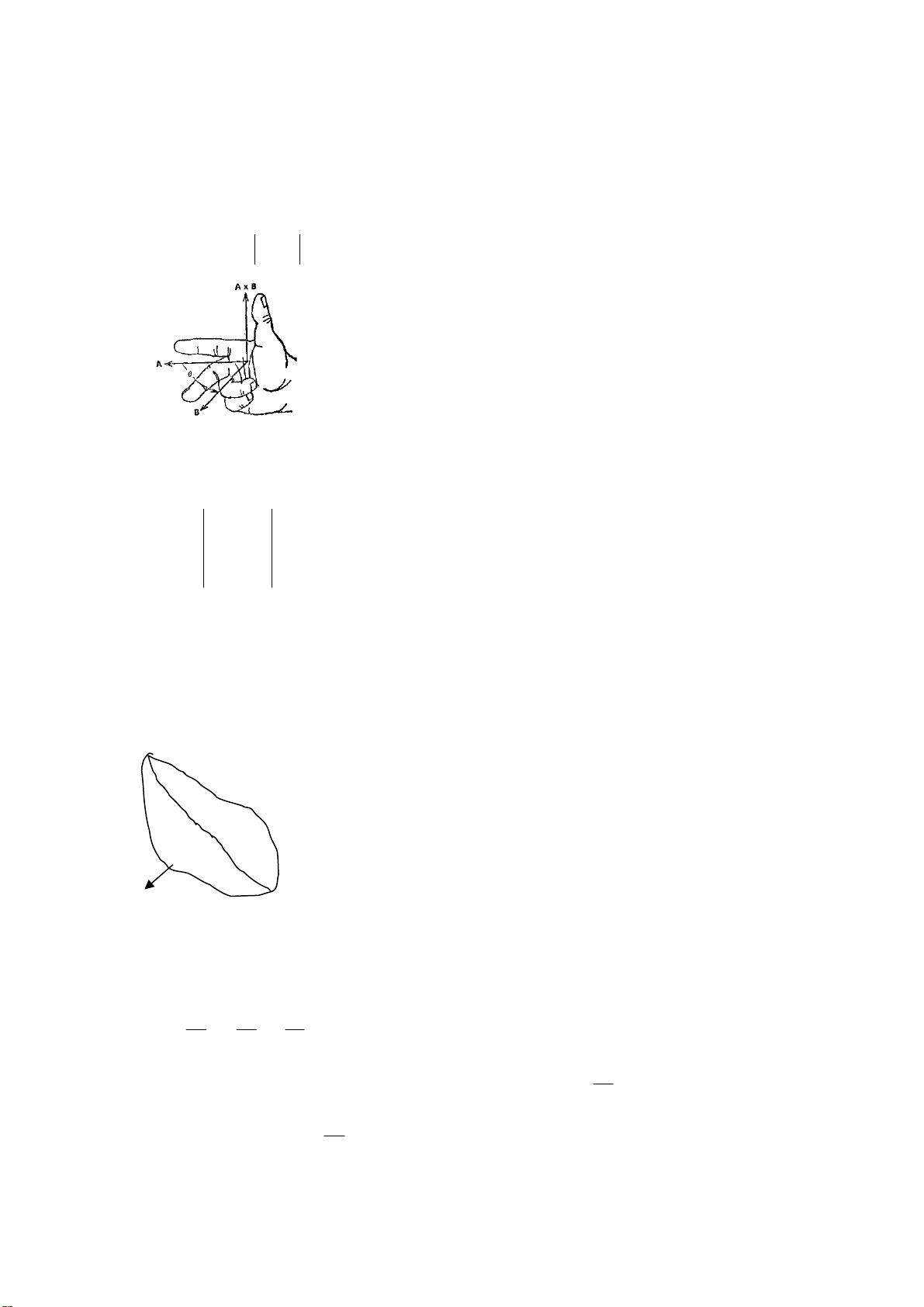
电磁场与波教案 矢量以及代数运算 1.1.1 矢量的基本概念 必修课：《矢量分析课》 矢量是既有大小又有方向的量，例如力、位移、速度等。 标量则是只有大小而无方向的量，例如质量、时间、温度等。 单位矢量： 上方带“^”符号的黑体字母表示,在直角坐标系中有一组基本单位矢量ˆ x，ˆ y，ˆ z。 电磁场与波课程是研究电磁现象的基本理论和应用的高级课程，涵盖了矢量分析、电磁波的传播、辐射以及电磁场与波的相互作用等多个领域。在本课程中，矢量分析是理解和计算电磁场与波现象的基础，它不仅包括矢量的基本概念，还涉及矢量代数运算、微分算子、梯度、散度和旋度等重要概念。 矢量的基本概念是本课程学习的基础。矢量是指既有大小又有方向的物理量，如力、位移和速度等，与之相对的标量则只有大小，如质量、时间和温度等。在直角坐标系中，我们通常用带有上标箭头的黑体字母来表示单位矢量，例如 \(\hat{x}\)、\(\hat{y}\) 和 \(\hat{z}\)。 矢量的加法和减法在物理意义上分别对应着场分量的叠加和空间位置矢量的差异。数学上，矢量的加减可以通过分量的方式进行。例如，两个矢量 \(\vec{A} = A_x\hat{x} + A_y\hat{y} + A_z\hat{z}\) 和 \(\vec{B} = B_x\hat{x} + B_y\hat{y} + B_z\hat{z}\) 的和是 \(\vec{A} + \vec{B} = (A_x + B_x)\hat{x} + (A_y + B_y)\hat{y} + (A_z + B_z)\hat{z}\)。矢量的点乘和叉乘也是基本运算，点乘结果为标量，表示两个矢量的内积，而叉乘结果为矢量，表示两个矢量的外积。 在矢量函数的代数运算规则中，点乘和叉乘的运算具有明确的物理意义。例如，点乘可以用来求两个矢量的夹角的余弦值，叉乘则用于求得垂直于两个矢量所在平面的矢量，并且叉乘在直角坐标系中可以用来求面积元素的大小。 微分算子 \(\vec{\nabla}\) 是一个“符号”矢量，表示对空间坐标的偏导数操作，其在直角坐标系中的定义为 \(\vec{\nabla} = \hat{x}\frac{\partial}{\partial x} + \hat{y}\frac{\partial}{\partial y} + \hat{z}\frac{\partial}{\partial z}\)。梯度、散度和旋度则是微分算子 \(\vec{\nabla}\) 的特定运算形式，它们在电磁学中具有特殊的物理意义。 梯度是一个标量函数的偏导数构成的矢量，它指向标量函数值增加最快的方向，并且梯度与该方向上的切线方向垂直。梯度的概念在理解电势、温度场等标量场的空间变化时尤为重要。 散度是一个矢量场的点函数，它表示单位体积内源的强度，如果散度为零，则表示该点无源，即没有电荷。散度的概念在分析电荷分布和电场强度时是不可或缺的。高斯散度定理（也称为高斯定理）将散度与通过闭合曲面的通量联系起来，是电磁场理论中的一个基本定理。 旋度的概念则表明了一个矢量场是否是保守场，即环路积分是否为零。在右手坐标系中，旋度的拇指方向代表了旋转的方向，即旋度的矢量方向。旋度的计算和理解在分析电磁波的传播和场的旋转性质方面非常重要。 以上这些知识点是电磁场与波课程的基础，理解这些概念对于深入研究电磁场理论、波动方程以及电磁波的辐射和传播至关重要。此外，熟练掌握这些数学工具也是解决电磁场实际问题的前提条件。通过本课程的学习，学生将能够掌握处理电磁场问题的方法，以及运用这些概念来分析和设计各种电磁设备和系统。