推挽式变压器公式，推挽式变压器公式

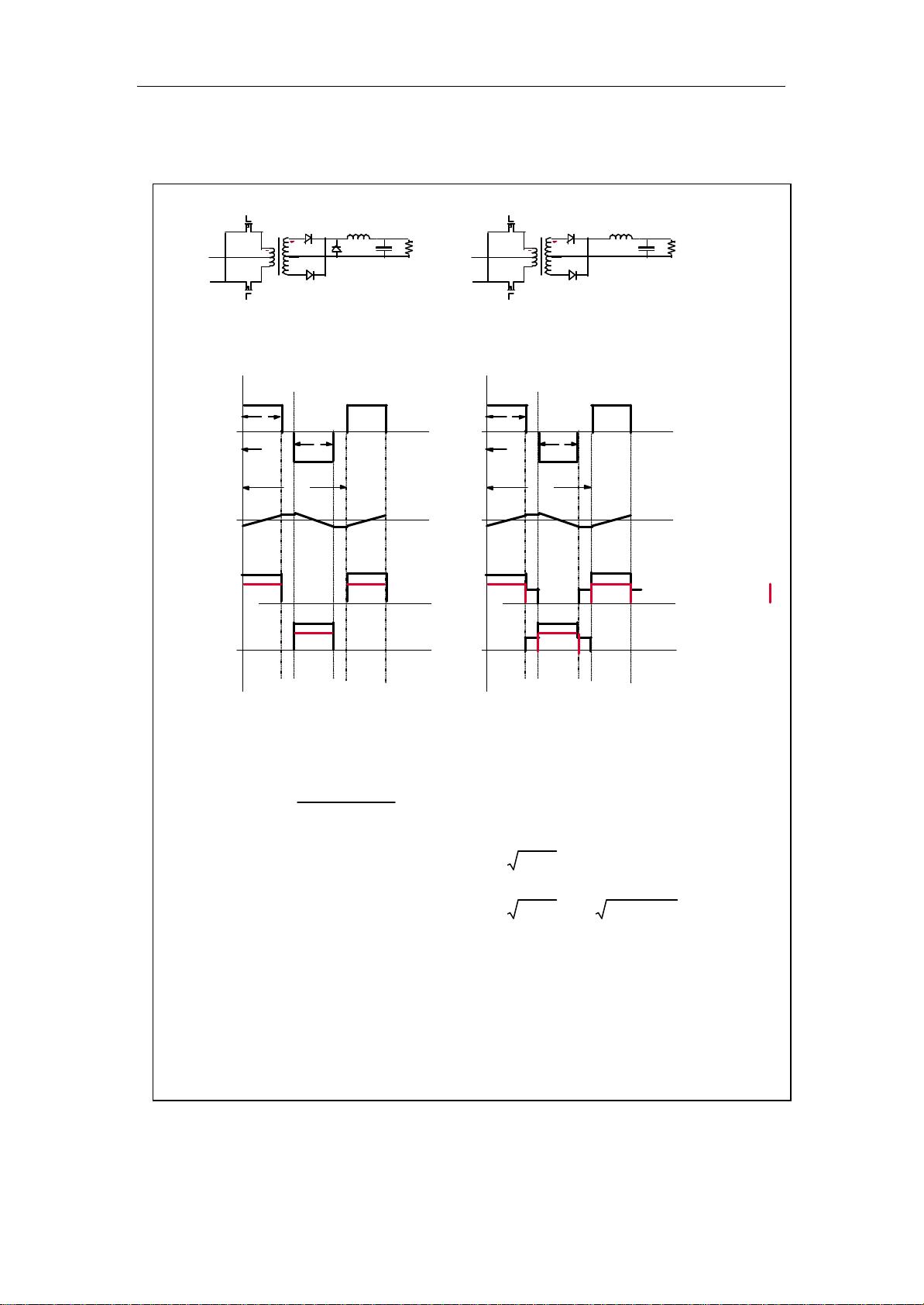
### 推挽式变压器设计公式解析 #### 一、引言 推挽式变换器是一种广泛应用在电力电子领域的转换装置，特别是在高频应用场合下。它能够有效地将输入电压转换成所需的输出电压，并且具备较高的转换效率。为了确保推挽式变换器能够稳定可靠地工作，正确设计其中的核心组件——高频变压器显得尤为重要。本文将基于提供的信息，详细介绍推挽式变压器的设计计算公式及其应用。 #### 二、推挽式变压器基本结构与原理 推挽式变压器的基本结构由两个开关管（S1和S2）、变压器、整流二极管（D1、D2、D3）以及滤波电感L和电容C组成。其中，开关管交替导通与截止，使得变压器原边绕组上的电压在正负半周期间变化，从而在副边产生相应的输出电压。这种结构的特点在于能够有效减少输入电源的谐波成分，提高系统的整体效率。 #### 三、关键参数及计算公式 ##### 1. 变压器设计中的核心参数 在设计推挽式变压器时，有几个核心参数非常重要，包括但不限于： - **最大负载功率**（\(P_{\text{max}}\)）：表示变压器能承受的最大功率。 - **最大磁密幅度**（\(B_{\text{max}}\)）：决定了变压器铁芯材料的选择。 - **电流密度**（\(J\)）：反映了变压器绕组导线的截面大小。 - **开关频率**（\(f_s\)）：影响变压器的尺寸和效率。 - **窗口系数**（\(K_w\)）：用于评估变压器的窗口利用率。 ##### 2. 面积积公式 面积积公式是推挽式变压器设计中最为核心的一个计算公式，它综合考虑了多个因素对变压器尺寸的影响。具体表达式如下： \[ A_{ca} = \frac{K_p K_T B_m}{f_s J} \eta_1 P_{\text{max}} \times 10^{-6} (\text{cm}^2) \] 其中： - \(A_{ca}\) 表示变压器的有效面积（平方厘米）。 - \(K_p\) 是拓扑系数，其值取决于具体的拓扑结构。 - \(B_m\) 是最大磁密幅度（高斯）。 - \(f_s\) 是开关频率（赫兹）。 - \(J\) 是电流密度（安培/平方毫米）。 - \(K_T\) 是拓扑系数，根据不同的拓扑结构有不同的计算方式。 - \(\eta_1\) 是在低限满载时的效率。 - \(P_{\text{max}}\) 是最大负载功率（瓦特）。 根据图示信息，我们可以进一步解析拓扑系数\(K_T\)的计算方法： - 当无续流二极管时（图(a)），拓扑系数\(K_T\)为： \[ K_T = D_{\text{max}} \] - 当有续流二极管时（图(b)），拓扑系数\(K_T\)为： \[ K_T = \frac{D_{\text{max}} + 2/\pi}{4} \] 其中，\(D_{\text{max}}\)表示最大占空比。例如，当最大占空比为0.45时，两种情况下的拓扑系数分别为0.67（无续流二极管）和0.68（有续流二极管）。 #### 四、实例分析 假设我们需要设计一个推挽式变压器，已知条件如下： - 最大负载功率\(P_{\text{max}} = 100W\) - 最大磁密幅度\(B_m = 1000G\) - 电流密度\(J = 2A/mm^2\) - 开关频率\(f_s = 100kHz\) - 拓扑系数\(K_T = 0.67\)（无续流二极管） - 效率\(\eta_1 = 0.9\) 代入面积积公式，可以计算出所需的变压器有效面积\(A_{ca}\)： \[ A_{ca} = \frac{0.67 \times 1000 \times 0.67}{100000 \times 2} \times 0.9 \times 100 \times 10^{-6} = 2.275 \times 10^{-4} \text{cm}^2 \] #### 五、结论 通过上述分析可以看出，面积积公式是推挽式变压器设计过程中一个非常重要的工具，它能够帮助设计者综合考虑多种因素，最终确定出合适的设计方案。对于不同的应用场景和需求，选择合适的参数组合是非常关键的。未来的研究可以进一步探索如何优化这些参数，以提高推挽式变压器的整体性能。