
1
1
Gernot Hoffmann
1. CIE Chromaticity Diagram (1931) 2
2. Color Perception by Eye and Brain 3
3. RGB Color-Matching Functions 4
4. XYZ Coordinates 5
5. XYZ Primaries 6
6. XYZ Color-Matching Functions 7
7. Chromaticity Values 8
8. Color Space Visualization 9
9. Color Temperature and White Points 10
10. CIE RGB Gamut in xyY 11
11. Color Space Calculations 12
12. Matrices 17
13. sRGB 23
14. Barycentric Coordinates 24
15. Optimal Primaries 25
16. References 27
Appendix A Color Matching 29
Appendix B Further Explanations for Chapter 5 30
Appendix C Compare Primaries sRGB and Adobe RGB 31
CIE Color Space
Contents

2
2
CIENTSC sRGB
AdobeRGB
380
460
470
475
480
485
490
495
500
505
510
515
520
525
530
535
540
545
550
555
560
565
570
575
580
585
590
595
600
605
610
620
635
700
0. 0 0. 1 0.2 0. 3 0.4 0. 5 0.6 0. 7 0.8 0. 9 1.0
0. 0
0. 1
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1. 0
x
y
1. CIE Chromaticity Diagram (1931)
The threedimensional color space CIE XYZ is the basis for all color management systems.
This color space contains all perceivable colors - the human gamut. Many of them cannot be
shown on monitors or printed.
The twodimensional CIE chromaticity diagram xyY (below) shows a special projection of the
threedimensional CIE color space XYZ.
Some interpretations are possible in xyY, others require the threedimensional space XYZ or
the related threedimensional space CIELab.
Purple line
Wavelengths in nm
sRGB uses ITU-R BT.709 primaries
Red Green Blue White
x 0.64 0.30 0.15 0.3127
y 0.33 0.60 0.06 0.3290
AdobeRGB(98) uses Red and Blue
like sRGB and Green like NTSC
CIE-RGB are the primaries for color
matching tests: 700 /546.1/435.8nm
3
3
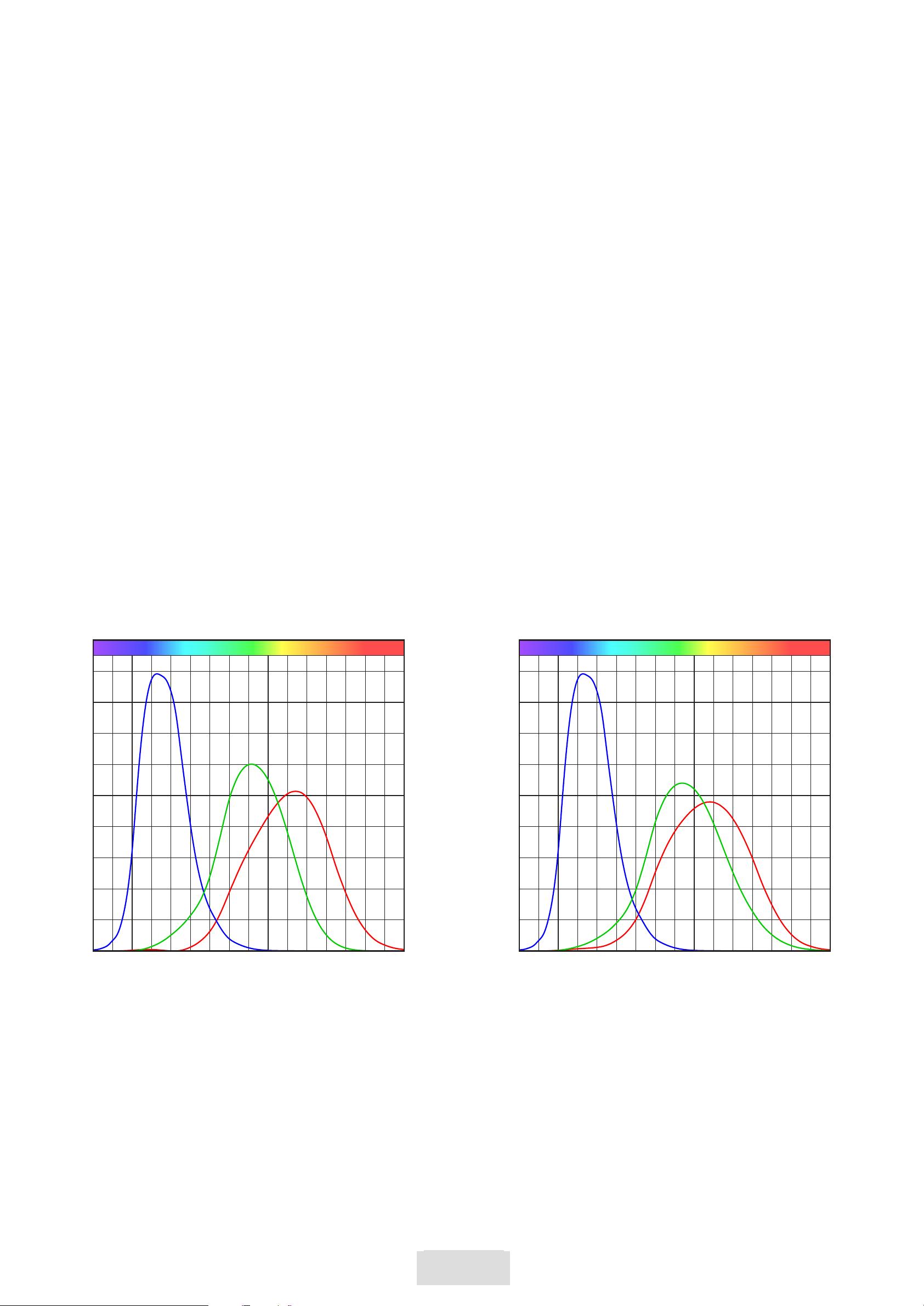
2. Color Perception by Eye and Brain
The retina contains two groups of sensors, the rods and the cones. In each eye are about 100
millions of rods responsible for the luminance. About 6 millions of cones measure color. The
sensors are already ’wired’ in the retina – only 1 million nerve fibres carry the information to
the brain.The perception of colors by cones requires an absolute luminance of at least some
cd/m
2
(candela per squaremeter). A monitor delivers about 100 cd/m
2
for white and 1 cd/m
2
for black.
Three types of cones (together with the rods) form a tristimulus measuring system. Spectral
information is lost and only three color informations are left. We may call these colors blue,
green and red but the red sensor is in fact an orange sensor.
The optical system is not color corrected. It would be impossible to focus simultaneously for
three different wavelengths. The overlapping sensitivities of the green and the red sensor may
indicate that the focussing happens mainly in the overlapping range whereas blue is generally
out of focus. This sounds strange, but the gap for image parts on the blind spot is corrected
as well – another example for the surprising features of eye and brain.
These diagrams show two of several models for the cone sensitivities. These and similar func-
tions cannot be measured directly – they are mathematical interpretations of color matching
experiments.
The sensitivity between 700nm and 800nm is very low, therefore all the diagrams are drawn
for the range 380nm to 700nm.
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
380 420 460 500 540 580 620 660 700nm
p1
_
p2
_
p3
_
λ
Cone sensitivities [3]
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
380 420 460 500 540 580 620 660 700nm
p1
_
p2
_
p3
_
λ
Cone sensitivities [1]
4
4
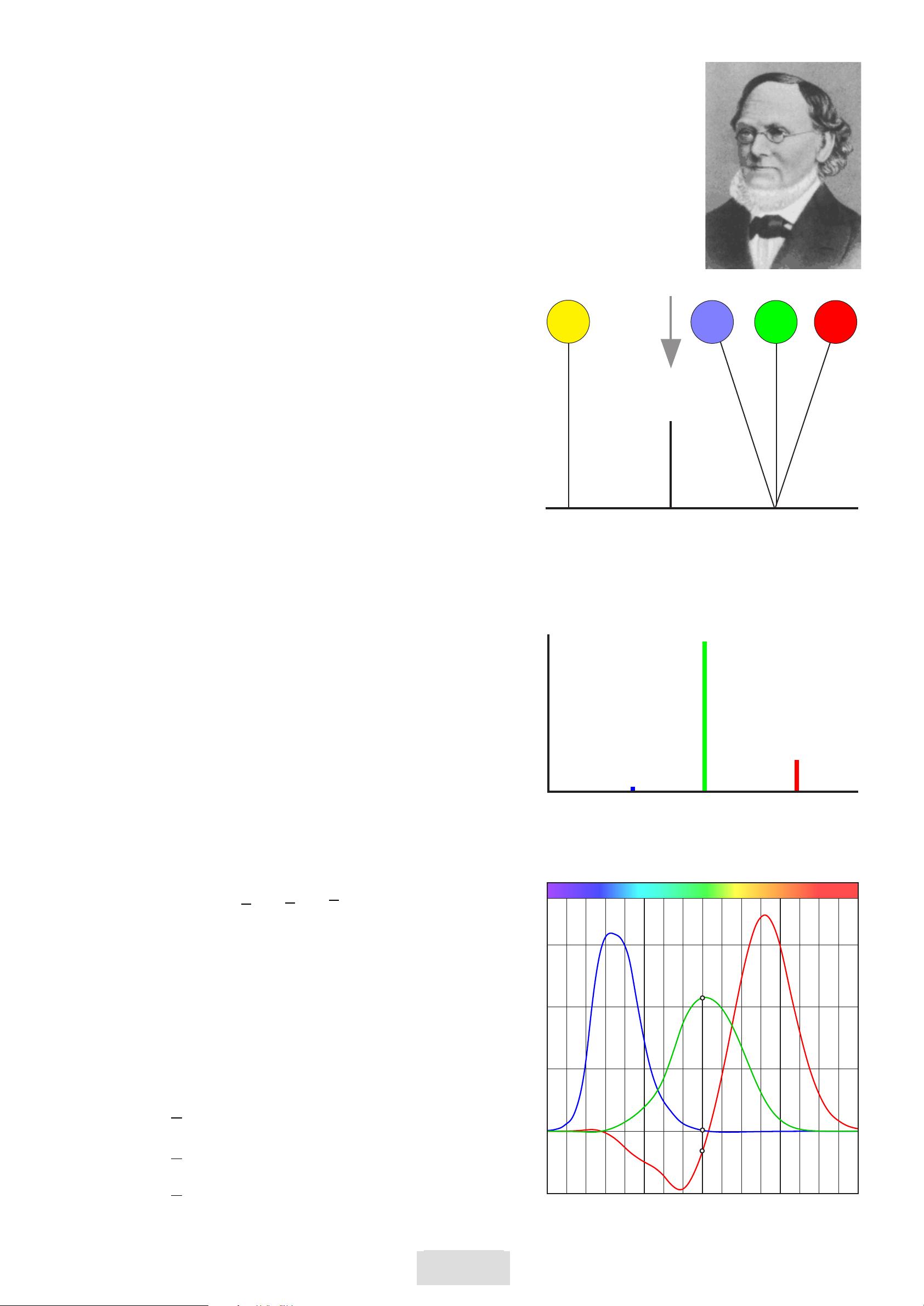
3. RGB Color-Matching
The color matching experiment was invented by
Hermann Graßmann (1809 – 1877) about 1853.
Three lamps with spectral distributions R,G,B and
weight factors R,G,B = 0..100 generate the color
impression C = RR + GG + BB.
The three lamps must have linearly independent
spectra, without any other special specification.
A fourth lamp generates the color impression D.
Can we match the color impressions C and D by
adjusting R,G,B? In many cases we can:
BlueGreen = 7R + 33G + 39B
In other cases we have to move one of the three lamps
to the left side and match indirectly:
Vibrant BlueGreen + 38R = 42G + 91B
Vibrant BlueGreen = - 38R + 42G + 91B
This is the introduction of ’negative’ colors. The equal
sign means ’matched by’. It is generally possible to
match a color by three weight factors, but one or even
two can be negative (only one for CIE-RGB) .
Data for the example are shown in Appendix A.
View
Color D Color C
The normalized weight factors are called CIE Color-
Matching Functions
r( )λ
,
g( )λ
,
b( )λ
.
The diagram shows for example the three values for
matching a spectral pure color (monochromat) with
wavelength λ=540nm. This requires a negative value
for red.
Color matching experiment
300 435.8 546.1 700.0 800
R,G,B
+4.5907
+1.0000
+0.0601
-0.1
0.0
0.1
0.2
0.3
0.4
380 420 460 500 540 580 620 660 700nm
r
_
g
_
b
_
λ
CIE Standard Primaries
RGB Color-matching functions
The CIE Standard Primaries (1931) are narrow band
light sources, monochromats, line spectra or delta
functions R,700nm, G,546.1nm and B,435.8 nm.
They replace the red, green and blue lamps in the
drawing above. In fact these sources were actually not
used – all results were calculated for these primaries
after tests with other sources.
R k P r d
G k P g d
B k P b d
=
=
=
∫
∫
∫
( ) ( )
( ) ( )
( ) ( )
λ λ λ
λ λ λ
λ λ λ
RGB colors for a spectrum P(λ) are calculated by
these integrals in the range from 380nm to 700nm
or 800nm:
5
5
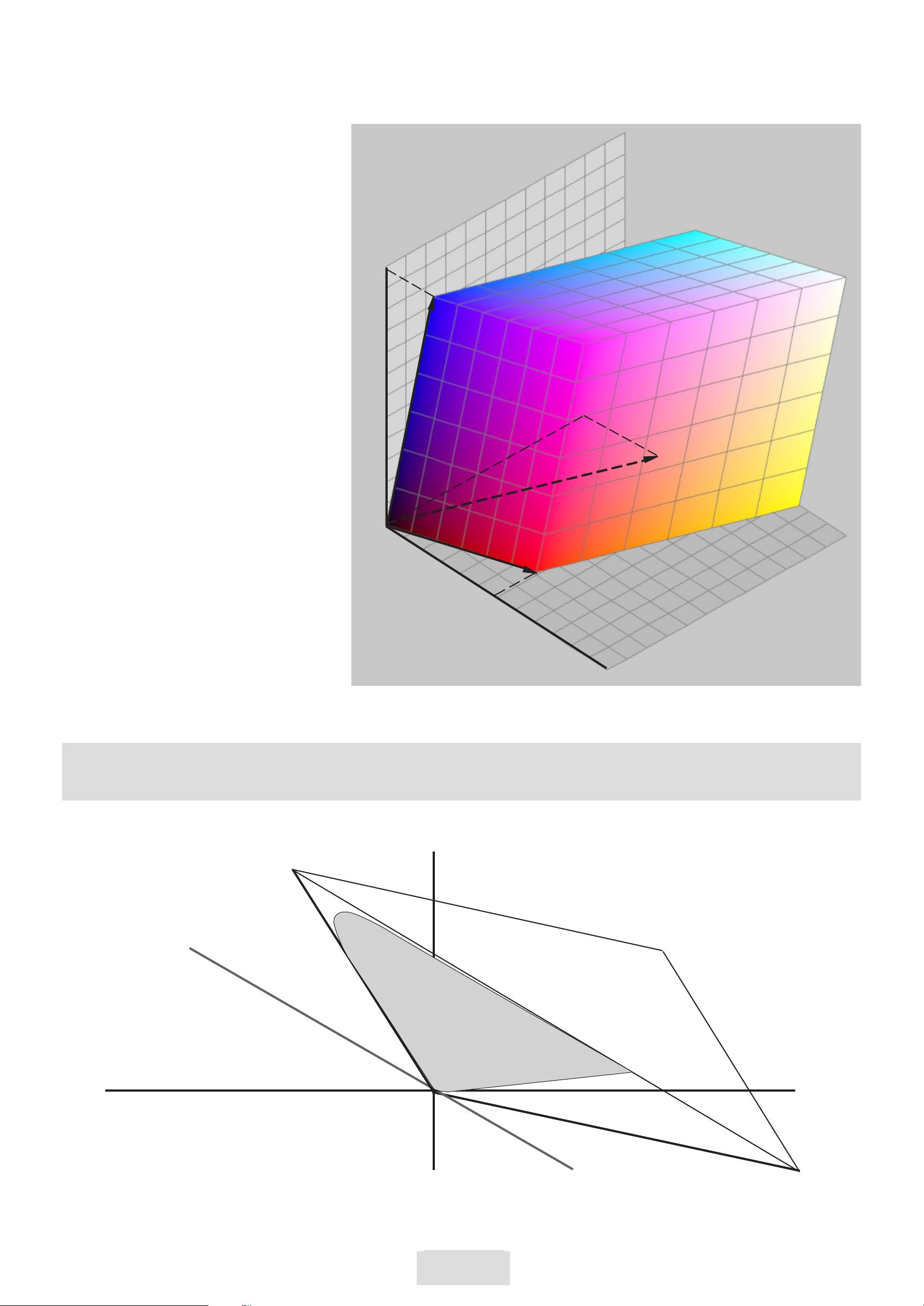
4. XYZ Coordinates
In order to avoid negative RGB
numbers, the CIE consortium
had introduced a new coordi-
nate system XYZ.
The RGB system is essentially
defined by three non-orthogonal
base vectors in XYZ.
The bottom image explains the
sitution for 2D coordinates R,G
and X,Y a little simplified.
The shaded area shows the
human gamut. A plane divides
the space in two half spaces.
The new coordinates X,Y are
chosen so, that the gamut is
entirely accessible for positive
values.
This can be generalized for the
3D space.
In the upper image the axes
XYZ are drawn orthogonally,
in the lower image the axes
RGB.
X
Z
X
R
Y
G
Plane
RGB base vectors and color cube in XYZ
2D visualization for RG and XY
R
0 49000
0 17697
0 00000
.
.
.
G
0 31000
0 81240
0 01000
.
.
.
B
0 20000
0 01063
0 99000
.
.
.
The coordinates of the base vectors in XYZ (coordinates of the primaries as shown above)
for any RGB system are found as columns of the matrix C
xr
in chapter 11.















评论0