数字信号处理答案详解

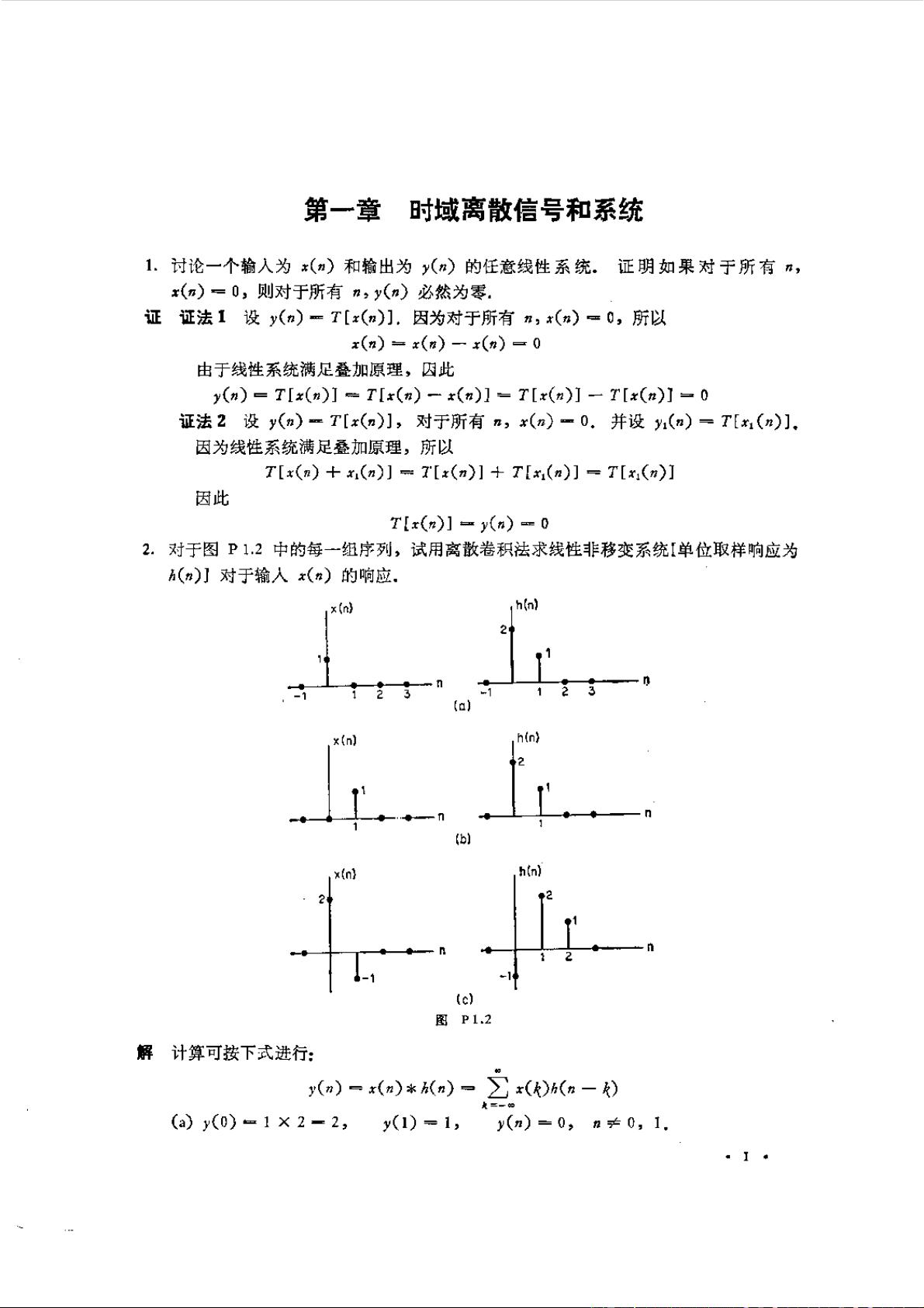
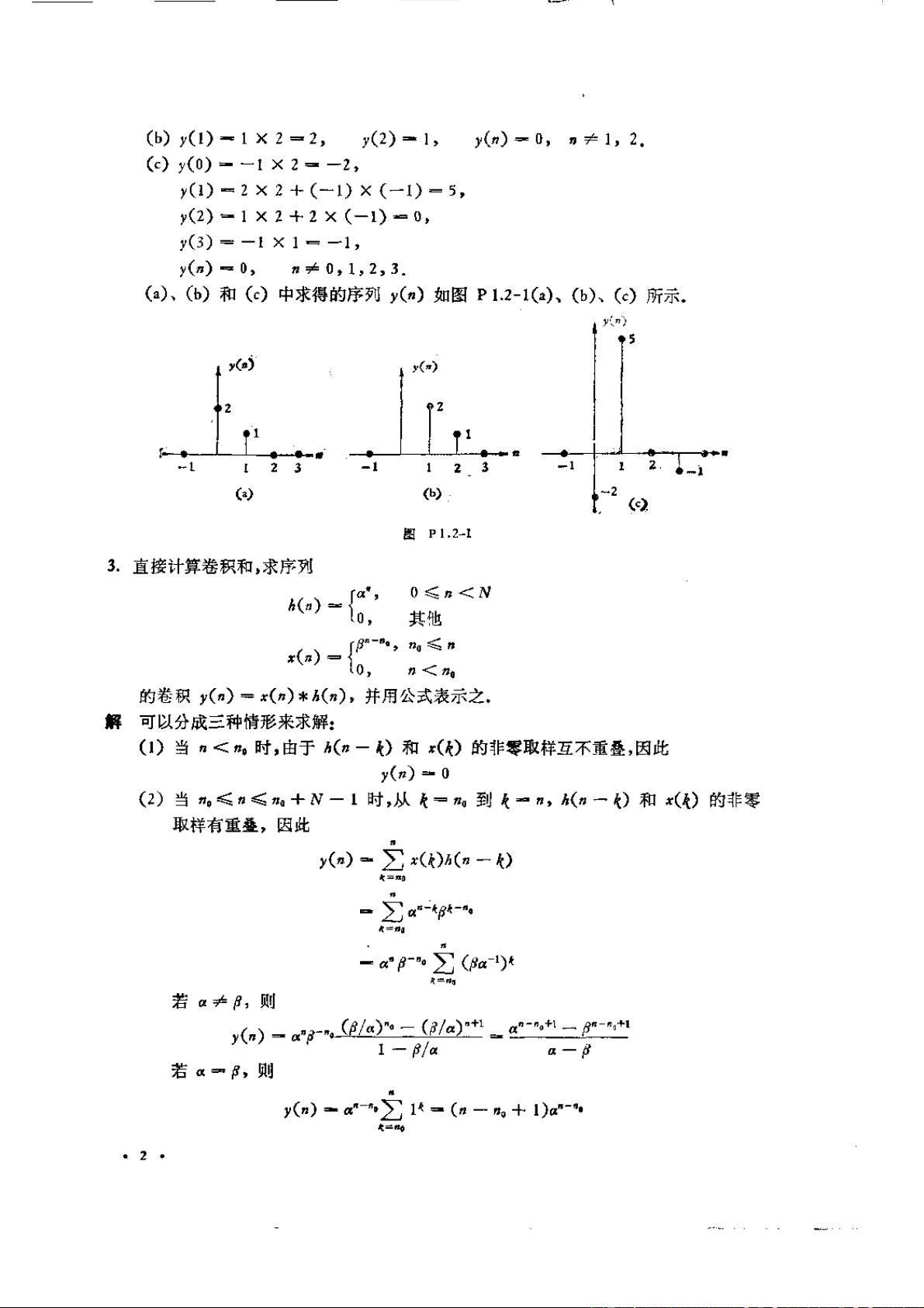
数字信号处理是现代通信、音频处理、图像处理等多个领域不可或缺的技术。奥本海默的经典数字信号处理教材不仅详细介绍了理论知识，还通过习题加深理解，适合自学。接下来，我们将详细解读上述数字信号处理的相关知识点。 时域离散信号和系统中，我们接触到基础的概念，如线性系统。线性系统的一个重要特性是叠加原理，即系统的输出是输入信号的线性组合。在线性时不变系统中，系统对输入信号的响应可以通过卷积运算来描述。卷积运算可以使用离散卷积公式计算，例如 y(n) = x(n) * h(n) = Σ x(k)h(n-k)，其中求和是对所有可能的k值进行的。这里的关键在于理解线性系统和叠加原理之间的联系，并掌握卷积运算的计算方法。 在数字信号处理中，离散卷积运算常常用于分析线性系统的响应。例如，对于具有单位取样响应h(n)的线性系统，输入信号x(n)通过系统的输出响应y(n)可以通过卷积运算求得。图p1.2中给出的序列，通过离散卷积运算，可以得到对应的输出序列y(n)。在求解过程中，需要考虑序列的边界条件，如序列长度小于N、等于N和大于N时的卷积和计算方法。 进一步地，对于给定的序列，可以利用离散卷积性质来求解系统的输出。例如，考虑单位取样响应的离散时间系统，输入信号与系统响应的卷积结果即为系统的输出。此外，可以通过直接计算卷积和的方式，求解序列z(n)与单位取样响应h(n)的卷积，得到输出信号y(n)。在计算时，需要根据卷积定理处理三种不同情况：当n小于0、n在0到N-1之间，以及n大于等于N时的情况。 除此之外，数字信号处理中经常需要证明某些性质，比如卷积的性质。例如，离散卷积的交换律、结合律和加法分配律。交换律表明两个序列的卷积与卷积顺序无关；结合律说明卷积运算符合结合性质；加法分配律表明卷积运算对序列的加法操作满足分配律。这些性质在简化计算和理解信号处理系统中非常重要。 在习题中也探讨了指数序列与卷积的关系，例如对于指数序列<(n)=a^n，其卷积的性质也得到了证明。指数序列的卷积结果同样遵循离散卷积的运算规则，并可以利用卷积的性质推导出新的序列。 以上分析涵盖了数字信号处理中的诸多知识点，如线性系统的叠加原理、离散卷积的计算、以及离散卷积性质的证明等。掌握这些基础知识点对于学习数字信号处理具有至关重要的作用。理解了这些概念和性质，就能够更好地应用于数字信号处理的实践中，比如在数字图像处理、音频信号处理和通信系统设计等方面。在学习的过程中，我们可以通过不断地练习，加深对这些知识点的理解和应用能力。