没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

1
第四节 奈奎斯特稳定判据
2
一、辐角定理:
对于一个复变函数
式中-z
i
(i=1,2,…,m)为F(s)的零点, -p
j
(j=1,2,…,n)为F(s)的极点。
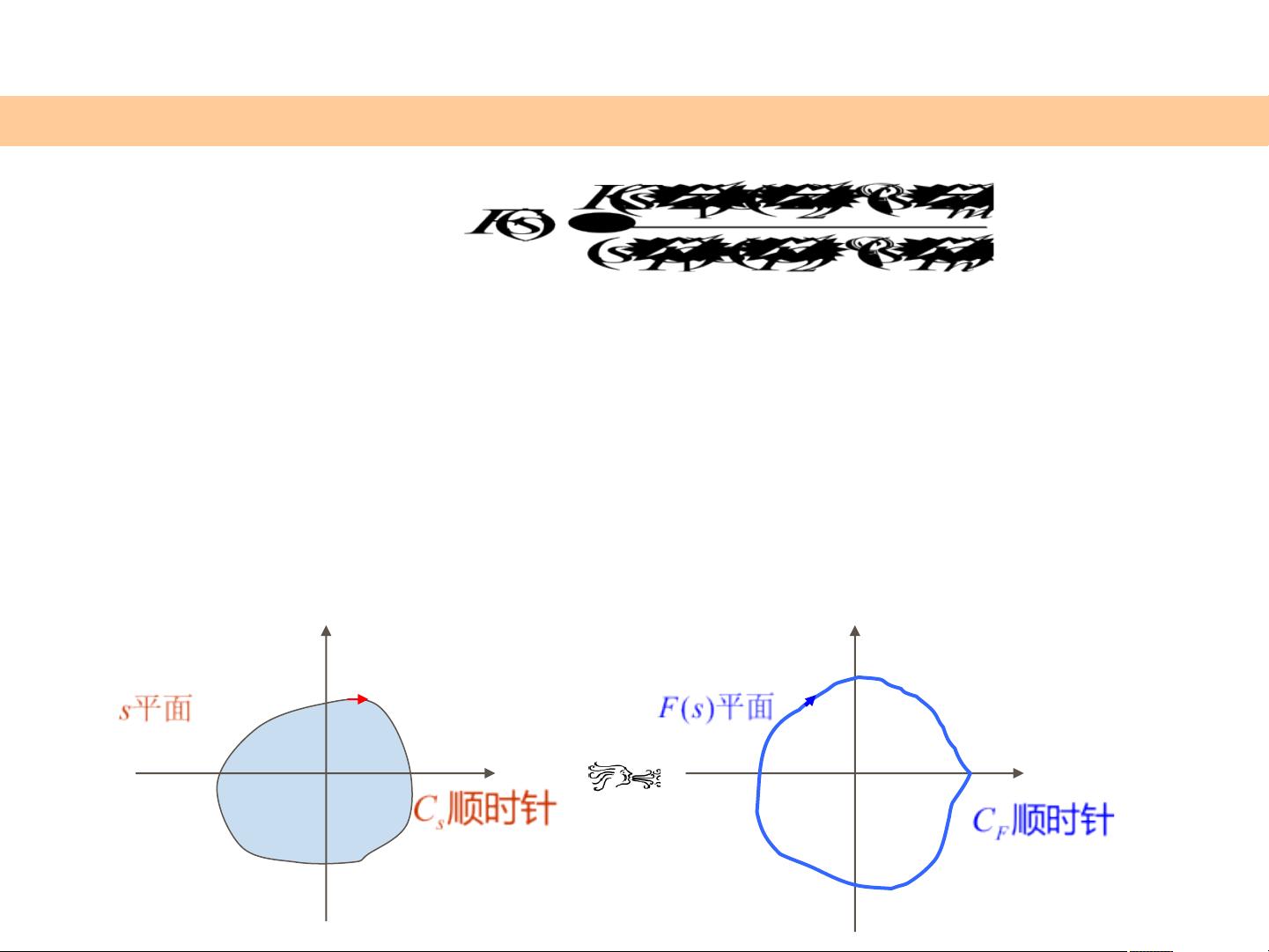
[柯西辐角原理]:S平面上不通过F(s)任何奇异点的封闭曲线C
S
包
围S平面上F(s)的Z个零点和P个极点。当s以顺时针方向沿封闭曲
线C
S
移动一周时,在F(s)平面上映射的封闭曲线C
F
将以顺时针方
向绕原点旋转N圈。N,Z,P的关系为:N=Z-P。
示意图
3
若N为正,表示C
F
顺时针运动,包围原点;
若N为0,表示C
F
顺时针运动,不包围原点;
若N为负,表示C
F
逆时针运动,包围原点。
函数F(s)是复变量s的单值函数,s可以在整个S平面上变化,对
于其上的每一点,除有限(n)个极点外,函数F(s)都有唯一的一个
值与之对应。
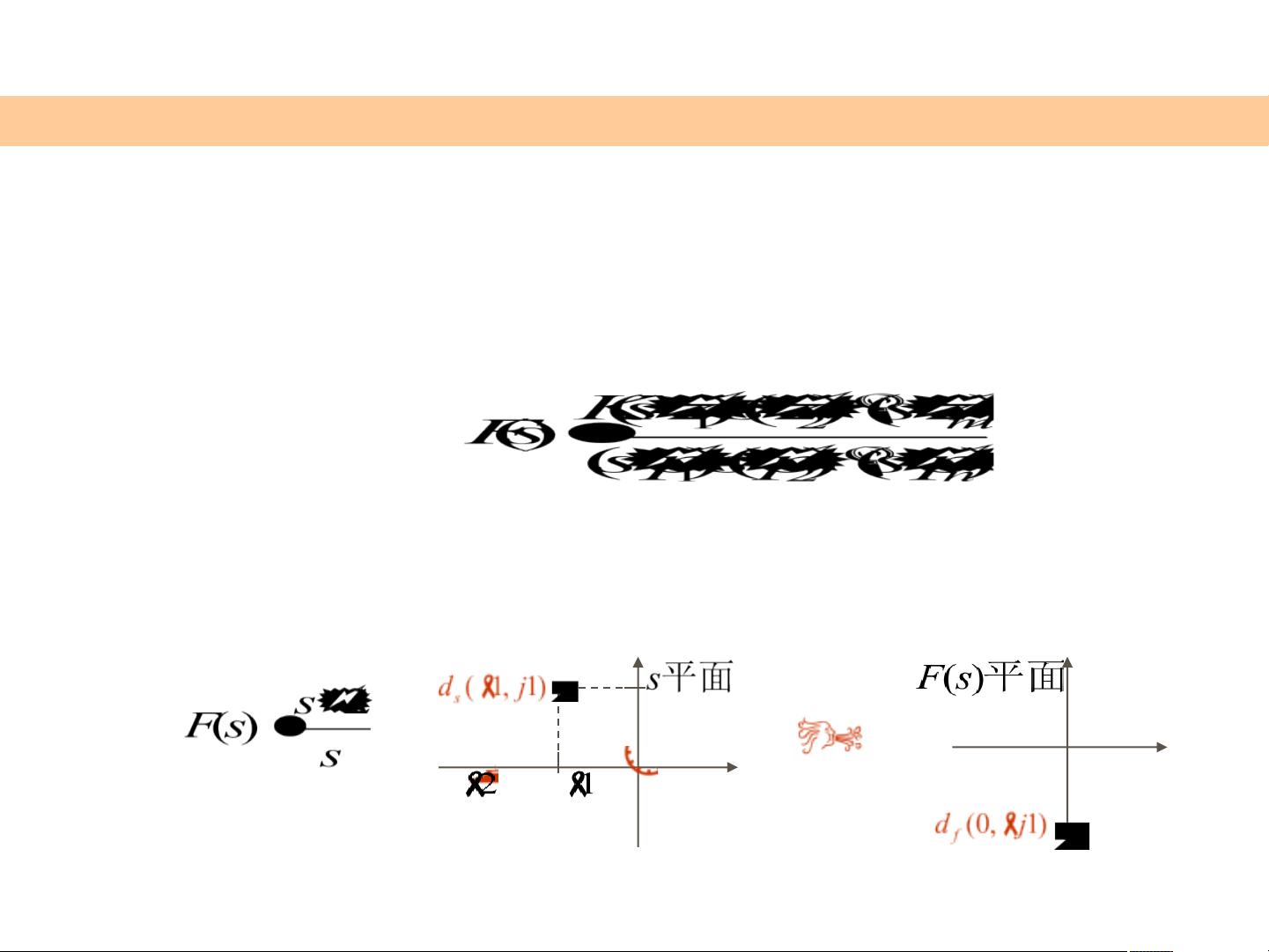
对于一个复变函数
[例]设:
4
F(s)的值域构成的复平面称为F(s)平面。其中S平面上的全部
零点都映射到F(s)平面上的原点;S平面上的极点映射到F(s)平面
上时都变成了无限远点。除了S平面上的零、极点之外的普通点
,映射到F(s)平面上是除原点之外的有限点。
注意,虽然函数F(s)从S平面到F(s)平面的映射是一一对应的,然
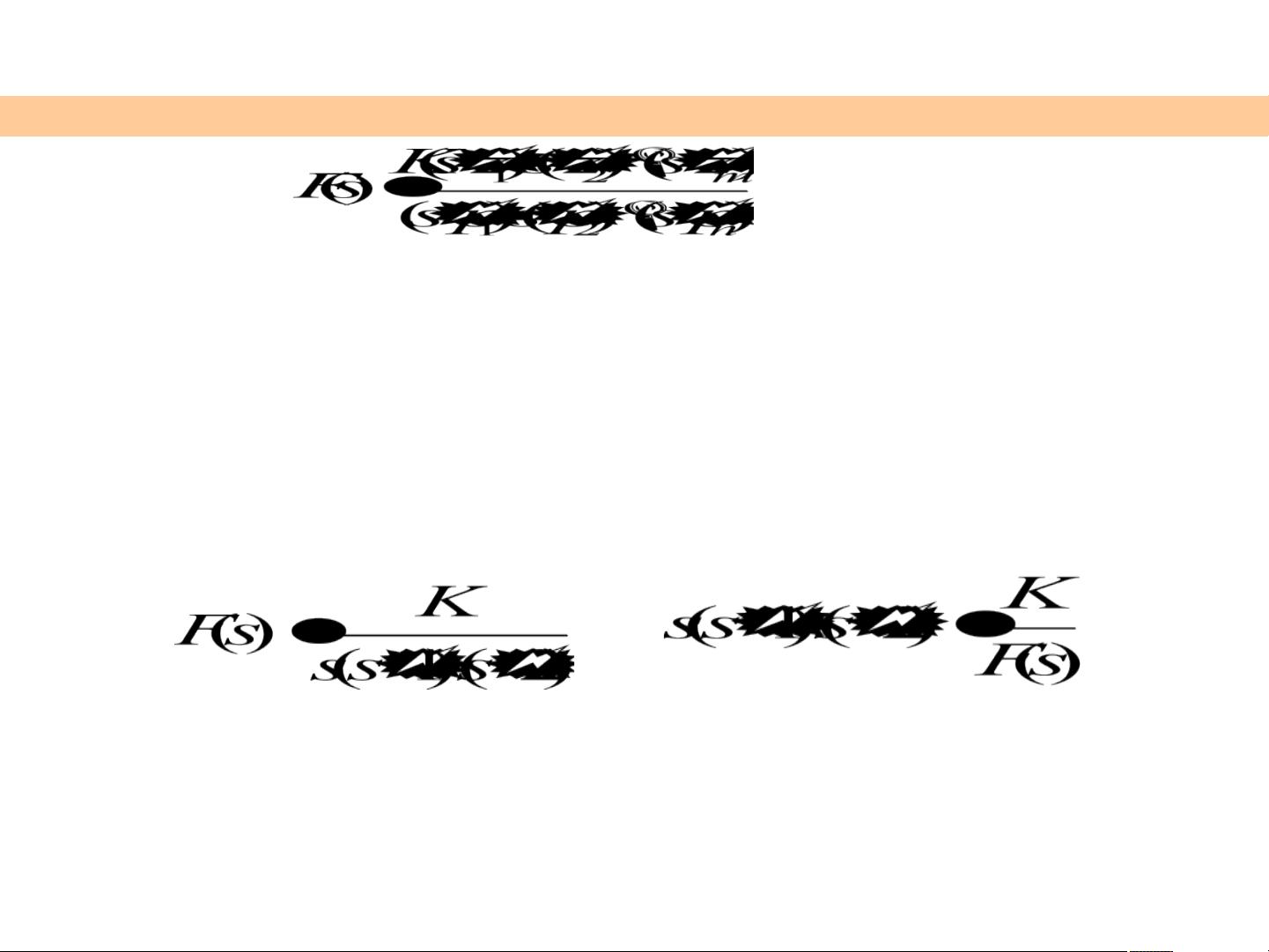
而逆过程往往并非如此。例如已知
这个函数在有限的S平面上除S=0,-1, - 2以外均解析,除此三
点外,S平面上的每一个S值在F(s)平面只有一个对应点,但是
F(s)平面上的每一个点在S平面上却有三个映射点。最简单的说
明方式就是将方程改写成
5
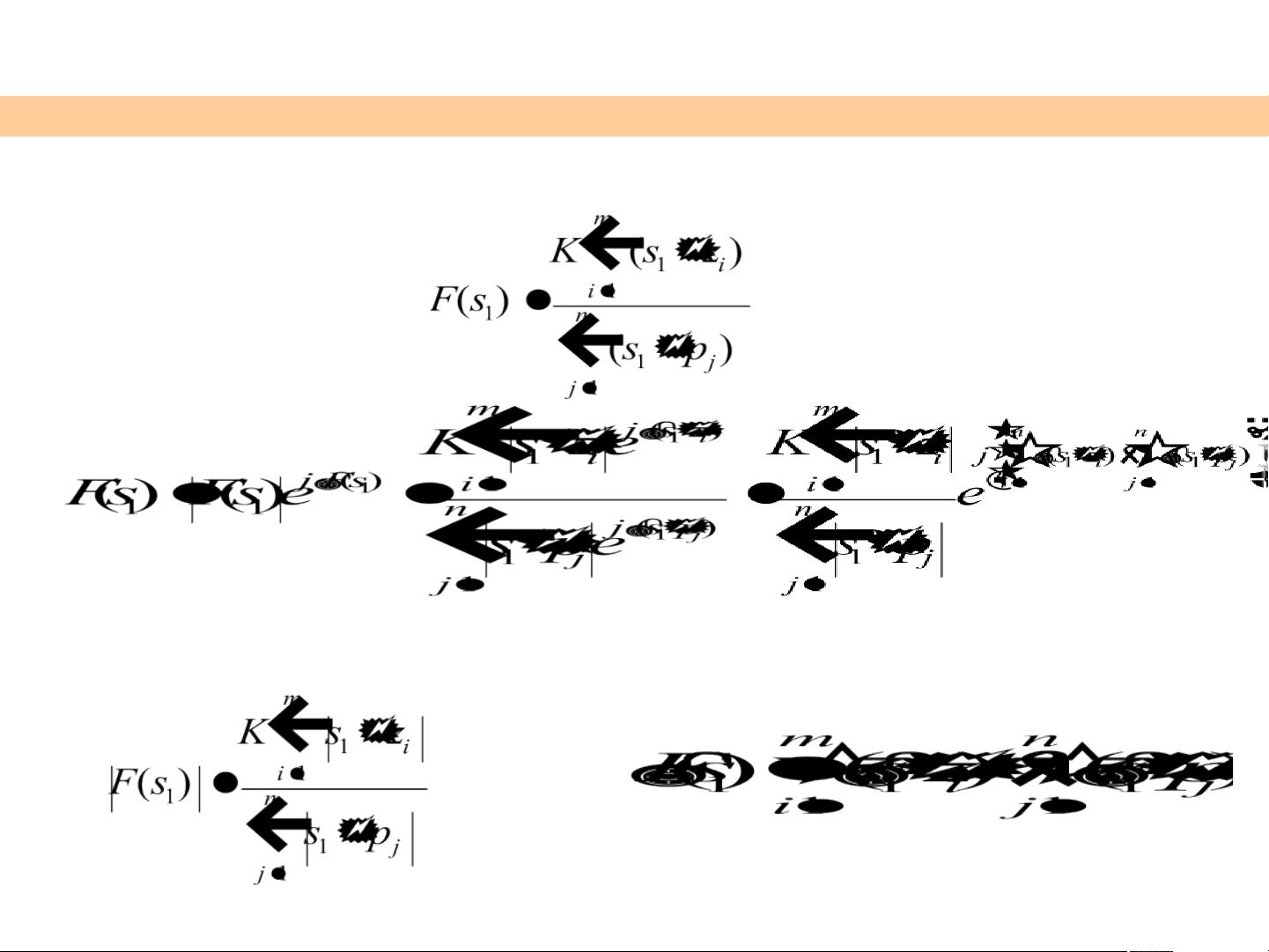
现考虑S平面上一点s
1
映射到F(s)平面上的点F(s
1
)可以用一个向量
来表示,即当
向量的幅值为
向量的相角为
剩余52页未读,继续阅读
资源评论

文档优选
- 粉丝: 95
- 资源: 1万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- F2的支付宝小程序版本.zip
- Windows winpe 迅雷单文件下载工具
- Discuz 论坛实现接口,以及结合 Discuz 的微信小程序.zip
- 基于动力学模型与RBF神经网络的沙堡持久度优化研究
- 基于周期性沙水细胞自动机模拟的最稳定沙堡地基几何形状研究与应用
- **********超分辨率模型***********
- chatgpt微信聊天小程序 java编写服务器,实现chatgpt接口的调用,微信小程序用于聊天 两者都基于webSocket进行通信.zip
- 海洋温度变化下鲭鱼与鲱鱼迁徙预测模型
- 气候变化下苏格兰地区鱼类迁移模式预测与渔业经济影响研究
- 气候变化下苏格兰小型渔业公司业务战略与鱼群迁移预测研究
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功