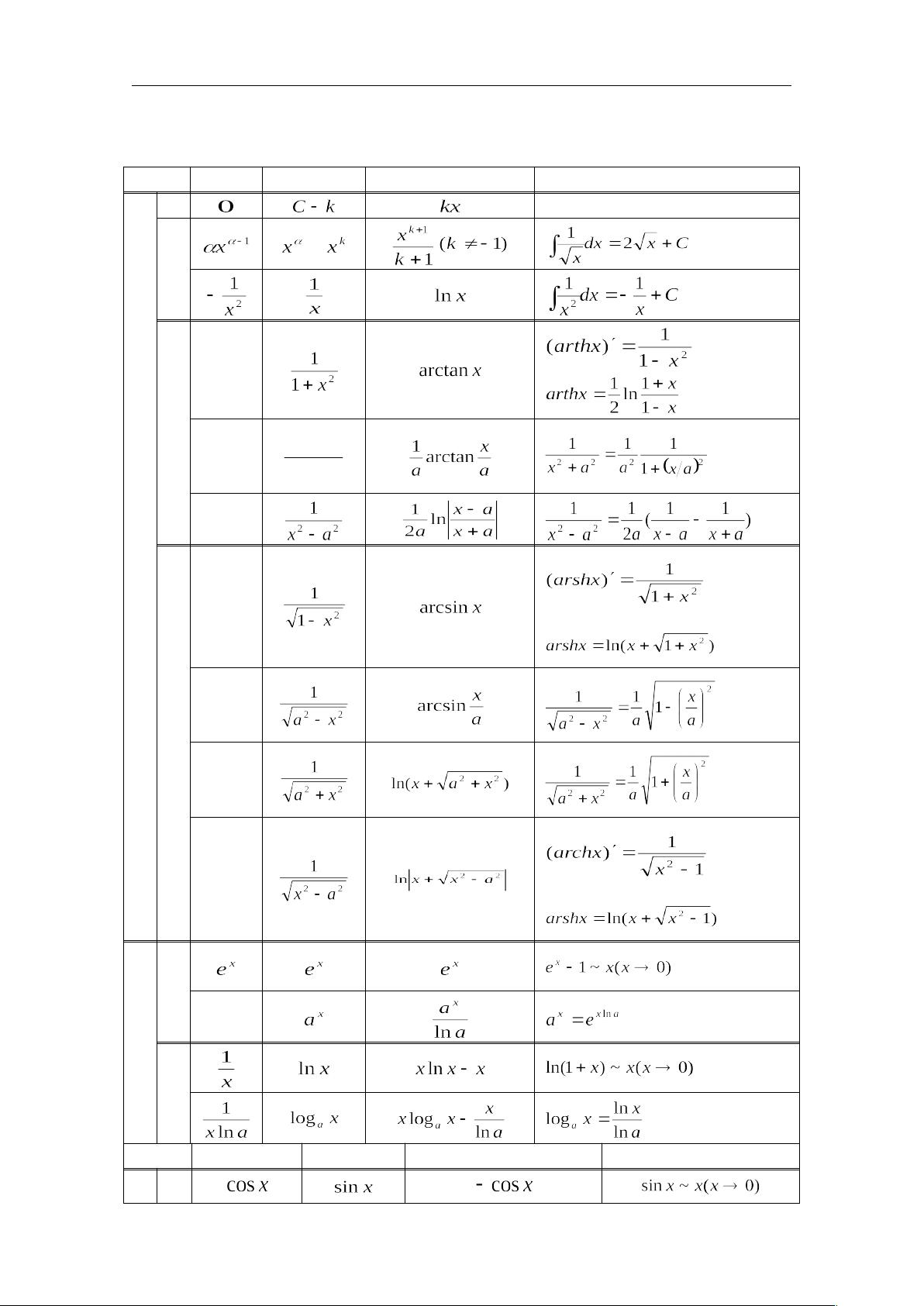
微积分是高等数学的基础，是研究函数变化率和求解累积问题的核心工具。在考研数学中，微积分公式是考生必须掌握的重点内容。本部分将详细介绍导数、函数和积分的相关概念及其公式，特别是幂函数的相关性质。
导数是微积分的基本概念，它描述了函数在某一点的瞬时变化率。对于一个函数f(x)，其在x处的导数定义为：
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
若存在，则称f可导。对于常见的幂函数，其导数规则如下：
- 对于 \( f(x) = ax^n \)，有 \( f'(x) = nax^{n-1} \)，这是幂函数的导数公式。
- 特殊情况，指数函数 \( f(x) = a^x \) 的导数为 \( f'(x) = a^x \ln a \)，其中ln a是自然对数。
- 对数函数 \( f(x) = \ln x \) 的导数为 \( f'(x) = \frac{1}{x} \)。
接下来，函数积分是微积分的另一核心概念，它是导数的逆运算。积分可以理解为函数图形下的面积或者物理过程的累积。基本积分公式有：
- 幂函数 \( f(x) = ax^n \) 的不定积分 \( \int ax^n dx = \frac{ax^{n+1}}{n+1} + C \)，其中C是积分常数，且n≠-1。
- 指数函数 \( f(x) = a^x \) 的积分 \( \int a^x dx = \frac{a^x}{\ln a} + C \)。
- 对数函数 \( f(x) = \frac{1}{x} \) 的积分 \( \int \frac{1}{x} dx = \ln |x| + C \)。
此外，还有三角函数和反三角函数的导数与积分：
- 正弦函数 \( \sin x \) 的导数是 \( \cos x \)，积分是 \( -\cos x + C \)。
- 余弦函数 \( \cos x \) 的导数是 \( -\sin x \)，积分是 \( \sin x + C \)。
- 反正弦函数 \( \arcsin x \) 的导数是 \( \frac{1}{\sqrt{1-x^2}} \)，积分则涉及到特殊积分技巧。
双曲函数如 \( \sinh x \) 和 \( \cosh x \) 也有相应的导数和积分规则，它们与三角函数有着密切的关系。
在考研准备中，理解和熟练应用这些公式至关重要。不仅要能够直接计算，还要能灵活变形和应用，解决实际问题。同时，熟悉这些公式也能帮助理解微积分的基本思想，为深入学习多元函数微积分、级数和微分方程等奠定坚实基础。因此，考生应反复练习，加深对微积分公式的理解，提升解题能力。
