应用回归分析试卷.doc

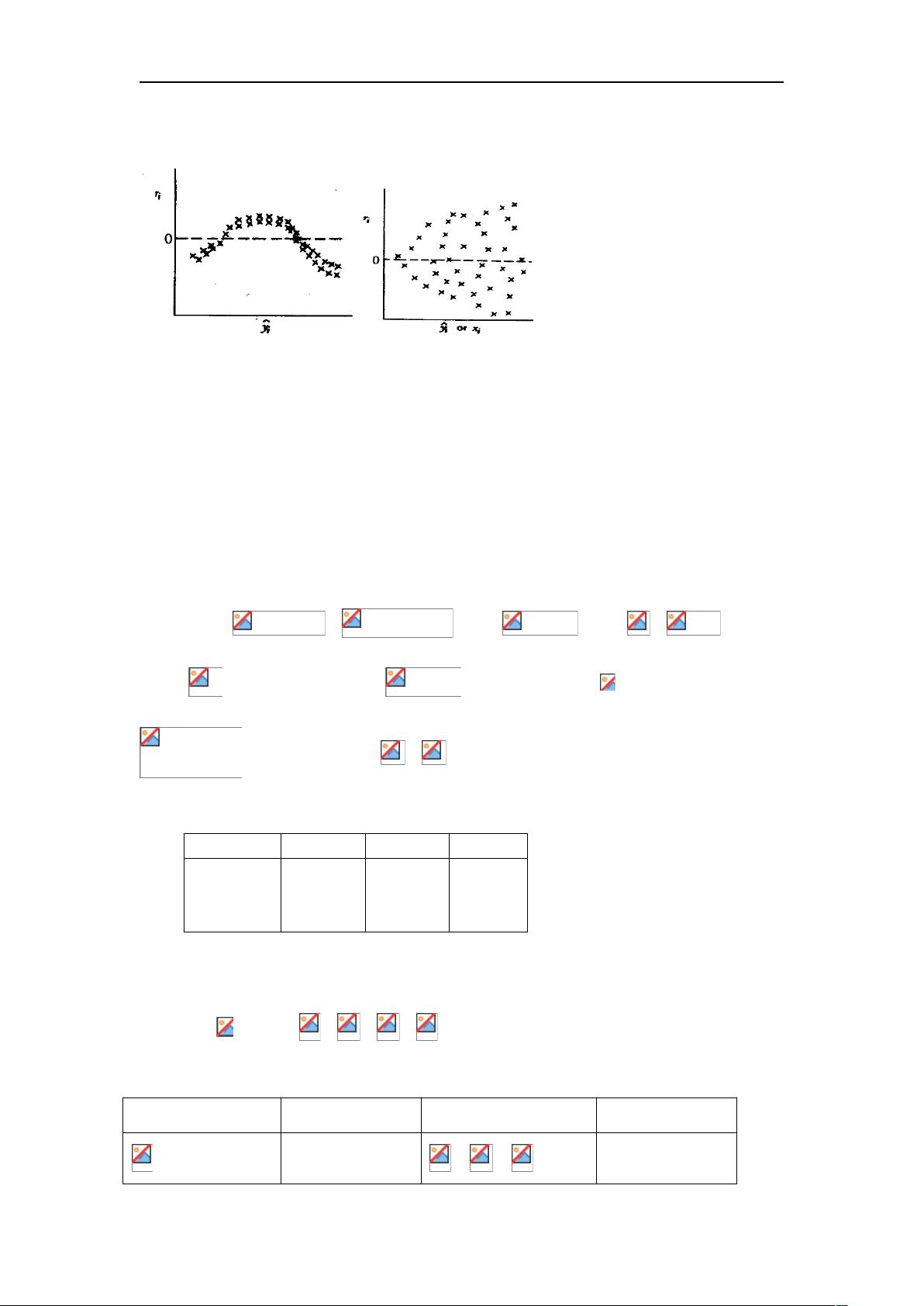
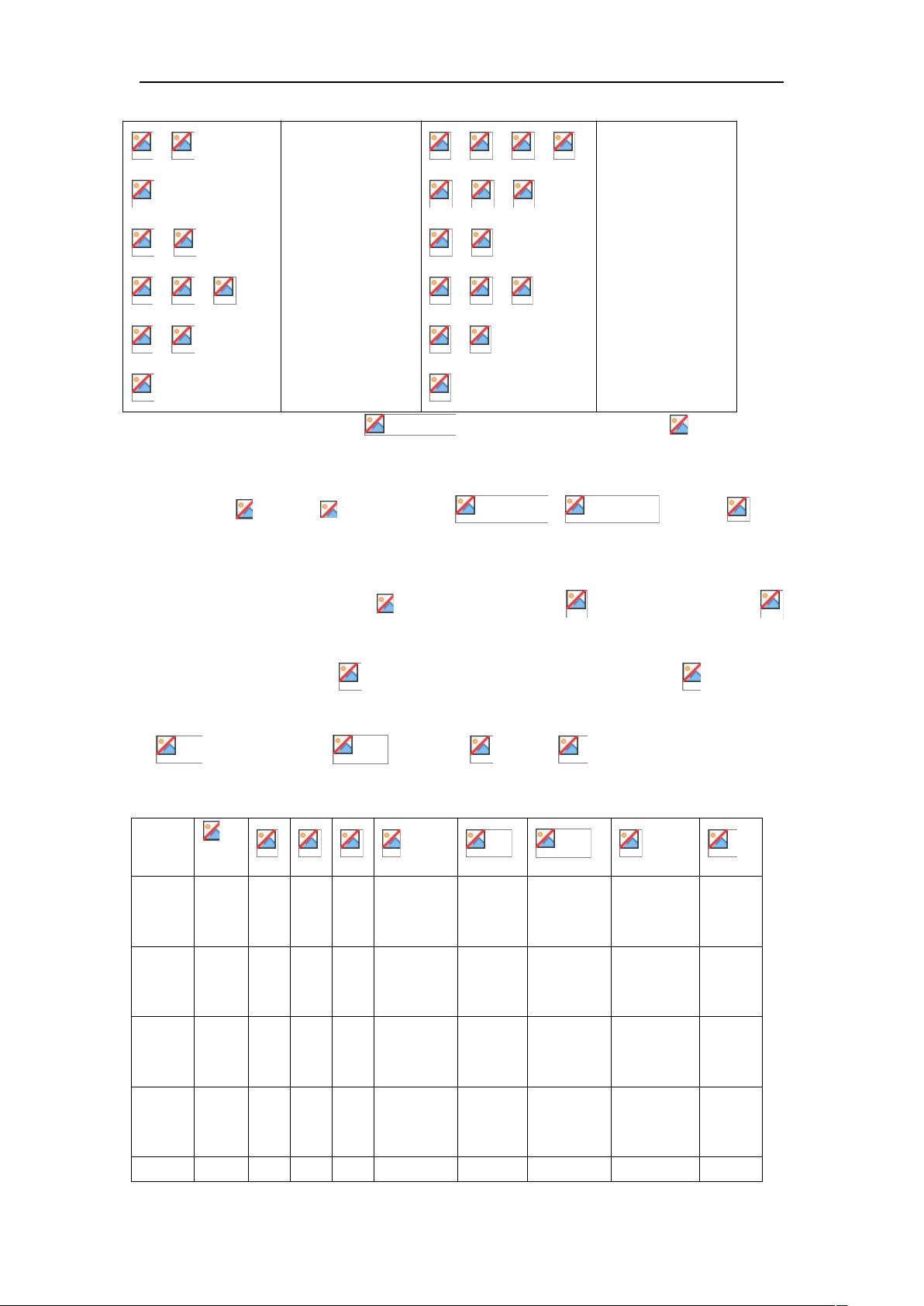
应用回归分析试卷 本试卷涵盖了应用回归分析的多个方面，包括一元线性回归、多元线性回归、回归诊断、误差方差稳定化、自相关性检验、岭迹图、AIC 值选择模型等。 一、选择题： 1. 对于一元线性回归，选项（A）“的最小二乘估计，都是无偏估计”是错误的。因为在一元线性回归中，_ONLY_最小二乘估计是无偏的，但不是所有的最小二乘估计都是无偏的。 2. 在回归分析中，假设诊断出异方差，常通过方差稳定化变化对因变量进行变换。如果误差方差与因变量的期望成正比，那么可通过logg变换将方差常数化。 3. 强影响点不一定是异常值。在多元回归中，回归系数显著性的 t 检验与回归方程显著性的 F 检验不是等价的。一般情况下，一个定性变量有 k 类可能的取值时，需要引入 k-1 个 0-1 型自变量。异常值的识别与特定的模型有关。 4. 残差图（C）表示误差序列是自相关的。 5. 岭迹图（A）表示在某一具体实例中最小二乘估计是适用的。 二、填空题： 1. 考虑模型，，其中，秩为，不一定，那么最小二乘估计是无偏估计。 2. 残差平方和=65965-66042=133，总的观察值个数=14，回归平方和的自由度=3。 3. 最优子集是模型，其中变量是最优的。 三、研究货运总量与工业总产值、农业总产值、居民非商品支出的线性回归关系： 1. 误差序列的自相关系数的估计值=0.876，假设存在自相关现象，常用的处理方法有迭代法、科克伦-奥克特迭代法。 2. 折线模型可表示为。 四、研究货运总量与工业总产值、农业总产值、居民非商品支出的线性回归关系： 1. 计算误差方差的无偏估计为3297/10=329.7，判定系数为0.933。 2. 对回归系数进行显著性检验，结果为F=12.447,p<0.01，表明回归系数显著。 3. 对回归方程进行显著性检验，结果为F=14.351,p<0.01，表明回归方程显著。 4. 诊断数据是否存在异常值，结果表明存在异常值，是关于自变量的异常值。 5. 回归方程为Y= -348.28 + 1.933X1 + 2.880X2 + 1.933X3，结合实际对问题作一些根本分析。